Оглавление:

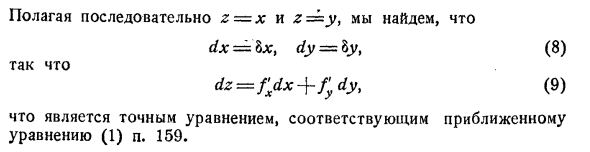

Дифференциалы
- Дифференциальный. Для математического анализа, особенно для геометрических приложений, в принципе очень удобно работать с уравнениями, включающими так называемые производные dx, dy, dz, а не с приращениями bx, на, hz функций x, y, z. Вы можете показать соотношение (1) в пункте 159 в виде уравнения с приращениями. Вернитесь к функции y == f (x) одной переменной x. Если / дифференцируемо, & Y = {/ ‘(*) + *} & *, (1) Где е стремится к нулю в точке bx. уравнение by = f (x) bx (2) Так что это «почти» правда. D6 До сих пор символ dy не имеет самостоятельного значения. Теперь мы согласны определить dy по уравнению dy = f (x) bx. (3)
Вот так dy = f (x) dx, (5) Разделив обе части уравнения (5) на dx, получим: (С) ду Здесь ~ означает не производную y до сих пор, а отношение производной dy и dx. Следовательно, символ ^ имеет двойное значение. Тем не менее, (6) справедливо для любого из двух значений слева, так что это не вызовет никаких неудобств. Теперь вернемся к соответствующим определениям, связанным с функцией z двух независимых переменных x и y. Определите дифференциал dz по уравнению dz = nx + fby. (7)
Если вы выберете функцию y = x в качестве y, вы получите dx = bx, (4) Людмила Фирмаль
| Дифференцирование функции от двух переменных | Определенные интегралы и площади |
| Теорема о среднем для функций от двух переменных | Определенный интеграл |
Примеры решения, формулы и задачи
| Решение задач | Лекции |
| Расчёт найти определения | Учебник методические указания |
- Предполагая непрерывные z = x и z = y, dx = bx, dy = by, (8) Вот так dz = fxdx + fydyt (9) Это точное выражение, соответствующее приближенному выражению (1) в пункте 159. Одна из характеристик уравнения (9) заслуживает отдельного упоминания. В §157 z = f (x> y), и если x и y являются функциями переменной t%, т.е. не зависят друг от друга, z является функцией только t, dz__dfdx, d / dy d’t ~~~ dx dt do dt ‘ Умножьте это уравнение на dt, принимая во внимание dx =% dt, dy =% dt, dz = §dt,
Мы получаем: dz = fxdx + f; dy, Внешний вид соответствует уравнению (9). Таким образом, выражение для dz по отношению к dx и dy такое же, как когда x и y не зависят друг от друга и как функция третьей переменной. Это замечание играет большую роль в приложении. И z является функцией двух независимых непостоянных х и у, dz = Ex-j-uly, Тогда A = f’x, что сразу следует за пунктом 159. Очевидно, что теорема и определение последних трех точек могут быть легко обобщены на функцию от любого числа переменных.
Дифференциальная запись имеет много практических преимуществ, особенно в геометрических приложениях. Людмила Фирмаль

