Оглавление:
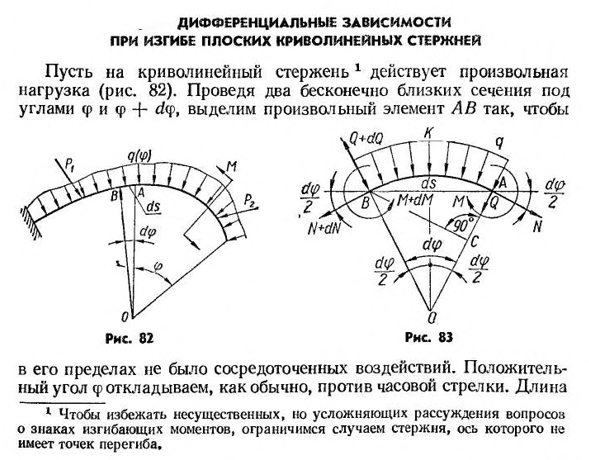


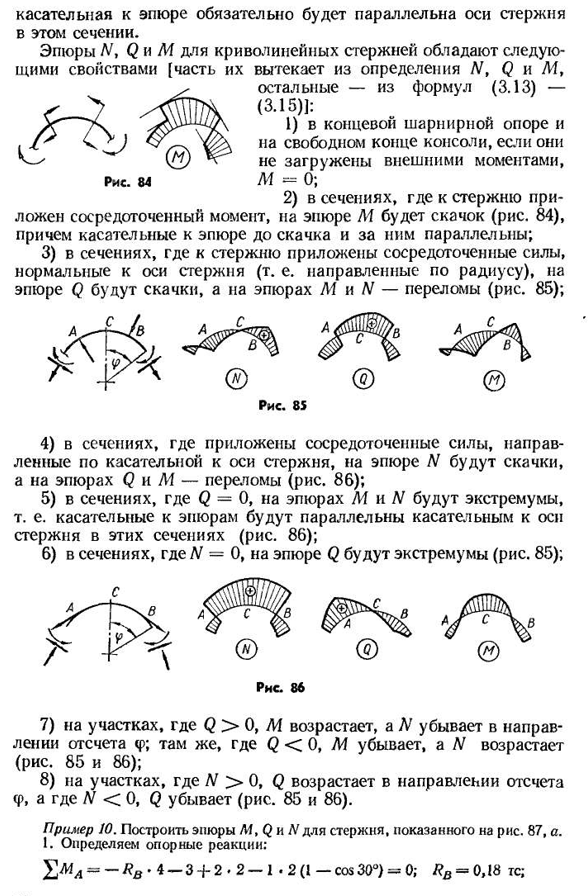



Дифференциальные зависимости при изгибе плоских криволинейных стержней
- На основе дифференциальных При изгибе плоской изогнутой палки Позвольте любой нагрузке воздействовать на изогнутый стержень 1 (Рис. 82). Поскольку мы нарисовали два бесконечно близких участка с углом, в области, где M увеличивается и n уменьшается в направлении отсчета0 Q увеличивается в направлении отсчета f,
а в области N<0,<2 уменьшается(рис. 85 и 86). Пример 10. Участок стержней M, Q и L’, как показано на рисунке. 87,1. Определите эталонную реакцию: 4 — 3 4 — 2 — 2 — 1• 2 (I-cos30°)=0; СП=0,18 ТС; 74y\M B= — 2 — 2 — 3 — 1. 2(1 + cos30°)+/?z-4=0; Yal=2,6 3TS; Vmc=- 0,18-2 — HB- 2 — 3 — 1 • 2 (1 — грех 30°) + 2,68 ■ 2 = 0; HB=0,5 TS. Проверять: =0,5-1 * cos60° = 0,5 — 0,5 = 0; — 0,18 + 2 4- 1 • cos30° — 2,68 = 2,87 =
0,01 шиш Погрешность в 0,4% обусловлена округлением. 2. Выберите Людмила Фирмаль
любой раздел: K -, сайт AD (0=0.18 грех Ф-0.5 соѕ Ф=-0 (Ф);(3-25) ■ = −0,18, потому что Ф-0,5 грех Ф=Л7 (Ф). 4. Используя формулу (3.21)—(3.23), создадим таблицу таблиц: значения L4, Q и/V.6-для раздела ads; табл. 7 — для постоянного тока; табл. 8-и на 1. Начиная с 1, цифры в квадратных скобках, помещенные в начале таблицы, указывают значение соответствующего столбца. Построим расчетные
вертикальные оси/и Y и Q(рис. 87, 6). 5. Это означает, что только в этом сечении касательные к участкам M и N будут перпендикулярны радиусу стержня. На графике N кривая, которая мысленно изображает вершины координат, дважды проходит через ноль в секциях DC и BC. Найти угловые координаты этих точек по формулам (3.22) и (3.23): DC2, 68cos F0-cos(F0-30°)= = 0;2,68 cos F0-cos0-cos3’J * cos F0-sin30° * sin f
- ()=0; 1,81 Fo=sin f=0;18sin P0-0,5 cos P0= = — (0,18 • 0,338 4-0,5 • 0,941) TC = −0.0 TC. 6. Отложим координаты QMaKC и QMHtl и нарисуем кривую графика (рис. 87, Б). 7. Проанализируем график с точки зрения общих свойств: а)A и b время/и=0 в стыке; о) приложим крутящий момент M и P поперечного сечения==3TC*m и график в эту величину скачка; д)сила в сечении Q=0 и в этой точке участка M и N являются касательными(по радиусу); е) в сечении f-F0 и P эти >o на блоке,
M увеличивается, a/V уменьшается(если двигаться вдоль стержня в направлении отсчета f, т. е. против часовой стрелки от точки); q<O на область действия силы CB, M уменьшается; I) значения Q и n участков A и B соответствуют значениям эталонной реакции. Таблица 6 Один. Два. Три. Четыре. Пять. 6 1 7 <G sin f COS f1-COS f M (f)=— 5 36 |4] М (ф)= =2.68•[2] Ш (Ф)= = 2.68•[3] ТС м ИС Ноль. Пятнадцать. Тридцать. Ноль. 0,259 0,500 Тысяча. 0.966 0.866 Ноль. 0.031 0.134 Ноль. 0.18 0.72 Ноль. 0.69 В 1,34 2.68 2.59 2.32 Таблица 7 Один. Два. Три. < Шесть. * Семь. Восемь. Ф°ф-30°ПЭ Ф соѕ Ф 51p позволяют вести съемку быстро(Ф—30°) Со$(Ф — — 30е)1-потому что Ф1-
это потому, что Х Х (ф-30°) Тридцать. Сорок пять Шестьдесят. Семьдесят пять. Людмила Фирмаль
Девяносто. Ноль. Пятнадцать. Тридцать. Сорок пять Шестьдесят. 0,500 0.707 0.866 0.966 Тысяча. 0.866 0.707 0,500 0,259 Ноль. Ноль. 0,259 0,500 0.707 0.866 Тысяча. 0, 9g6 0.866 0.707 0,500 0.134 0.293 0,500 0.741 Тысяча. Ноль. 0.034 0.134 0.293 0,500 Девять. Десять. Одиннадцать. Двенадцать. Тринадцать. Четырнадцать. Пятнадцать. f°5.36•[71 2•[8] М (S)==|9 1 — [10 —] ТС * м 2,68•[3] М (ф)= = Р21 — — /51TC 2.68•[4] Л/(Ф)=-[1 4 1 — — [6]ТС Тридцать. Сорок пять Шестьдесят. Семьдесят пять. Девяносто. 0.72 1,57 2.68 3.97 5.36 Ноль. 0.07 0.27 0.59 Из 1.00
Смотрите также:
| Построение эпюр для рам | Построение эпюр внутренних усилий для пространственных стержней |
| Построение эпюр для криволинейных стержней | Напряжения в сечении |

