Оглавление:







Дифференциальные зависимости при изгибе. некоторые особенности эпюр q и м
- Дифференциальная зависимость при изгибе. Некоторые особенности сюжета Q и M Его значение облегчает построение участка и позволяет в некоторой степени контролировать его правильность. Рассмотрим балку с любой нагрузкой(рис. 64, а). Распределенная нагрузка, которую мы согласны считать положенной- а б о б о Рис шестьдесят четыре Если она направлена вверх(такая нагрузка дает положительную составляющую изгибающего момента любого
сечения). Назначим на участок ПЭТ, пучка о\ОГ небольшие элементы сосредоточенной силы и момента. Он находится в равновесии под действием внешних нагрузок, поперечных сил и изгибающих моментов сечения и О2(рис. 64, Б). В общем случае Q и M изменяются вдоль оси луча, поэтому сечение Ot имеет Q (x) и M (x), а сечение O2 имеет Q (x) 4-clQ и M(x) 4-dM. Для вывода,
Как обычно, мы изобразим их положительно. От равновесного состояния Людмила Фирмаль
выбранного элемента, мы получим=М—М Г X в-(М+йд)=0 -,^м ОГ=М4-Qdx4-сохранить—(М4-ДМ)=0. Первое уравнение дает следующие условия (3.3) Из второго уравнения, если мы игнорируем срок действия 、 (Зл) Миз в формулах (3.3) и (3.4) выглядит следующим образом d’M dx2~ Кроме того, при рассеянии момента прочности Т кгс-см/м действует на рассматриваемый участок(рис. 64, Б), формула (3.4) принимает вид: (3-6) Выражения (3.3) и (3.5) не изменяются.
Соотношения (3.3)-(3.6) называются дифференциальными зависимостями при изгибе. Анализ примеров этих зависимостей и предыдущего абзаца позволяет установить некоторые особенности диаграммы изгибающих моментов и боковых сил:1. В областях, где отсутствует распределительная нагрузка, участок Q ограничивается прямыми линиями, параллельными основанию, обычно наклонными прямыми линиями(рис. 65). 2. В области, где равномерно
- распределенная нагрузка q приложена к балке, участок Q окружен наклонной прямой линией, а участок M окружен вторичной параболой(рис. 66). Так как участок М. — — — — — При построении на сжатом волокне выпуклая часть параболы направлена в направлении, противоположном направлению действия нагрузки q (рис. 67, С, Б). 3. В сечении Q равно 0, касательная участка M параллельна основанию участка (рис. 66 и 67). 4. В области Q>0 момент M увеличивается, то есть слева направо увеличивается положительная ордината графика M, а отрицательная
уменьшается(рис. 65, 66, сечения AC и BE) — в области Q<0 момент m уменьшается(рис. Разделы 65, 66, CD и DB). 55b. In участок, на котором концентрация приложена к пучку: а) по величине Q на графике произойдет скачок в направлении приложенной силы(на рис. 65 и 66 эти скачки отмечены толстыми линиями со стрелками); Б) будет разлом на участке М(рис. 68), точки разрушения, направленные против действия силы(см. Также разделы C., D и B на диаграмме. 65 и раздел В на рисунке. 66). 6. На участке, где сосредоточенный момент приложен к балке, происходит скачок к значениям этих моментов на графике M (на графике Q изменений нет). Направление скачка зависит от направления внешнего момента(рис. 69). Веток сюжета до и после прыжка
параллельны. Итак, рисунок показывает. 69 строка A / / CD / / EF (см. Также Людмила Фирмаль
рисунок. 61. Райс, семьдесят. 70, а). Это не применяется, если в одной точке приложены одновременно сила и момент (рис. 70, Б), — сила вызывает переломы, разрушает параллелизм. 567 если сосредоточенный момент приложен к балке на конце или торцевой опоре консоли, то в этом сечении изгибающий момент равен внешнему моменту (71, сечения В и с). Если концевая шарнирная опора или балка на конце консоли не нагружены в момент внешнего воздействия, то в ней имеется M=0. 65 и 66, раздел А и Е). 8. Таким образом, вертикальная ось участка Q пропорциональна касательно
й угла касания к участку M. Чтобы установить эти характеристики сюжета, рассмотрим следующее. Если нет распределенной нагрузки、 дуплексный Integrill я, пол у тройника: м(х)=СХ=Конст. И так оно и есть.» ~=<2=с дуплексный Где M (x)=C1X-| — C2. Д (3.7) Уравнения (3.7) и (3.8) доказывают свойство 1, поскольку если функция (3.7), то граф становится горизонтальной линией, а функция (3.8) обычно является наклонной линией (C4=#f0). Были доказаны и другие свойства. Однако следует отметить, что появление скачков на графике Q связано с введением условных понятий концентрации. Как уже говорилось, способность к концентрации мы рассматриваем как нагрузку,
распределенную по небольшой длине. Если балка нагружена такой реальной нагрузкой, то на графике Q и графике M (на рисунке отсутствует скачок к излому. 72). Это замечание относится и к действиям концентрированного внешнего момента. Рассмотрим более сложные случаи графиков Q и M. Пример 6. П А С П Е Д Е Н Н О й Н А Г У К О й, А З М Е Н Ы Й с и п л и н ы й н о м а к о н У на графике простой балки, нагруженной 73). Мы определяем реакцию поддержки. Результат всей распределенной нагрузки равен-g-и проходит через центр тяжести участка нагрузки.- Я Правое крыло зависимо от ключа на льне. И так оно и есть. 2^s=^Z—f-4 — =0; таким образом Поперечные силы
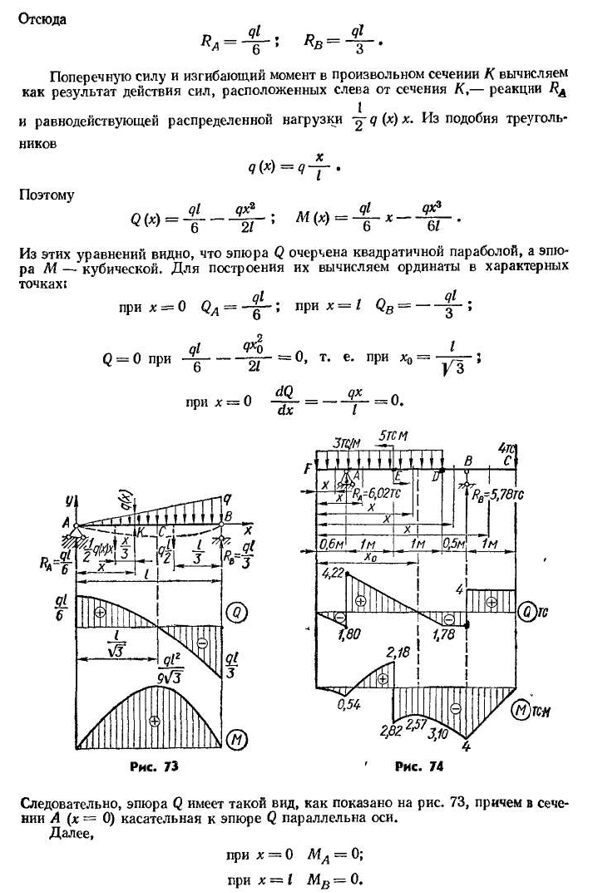
и изгибающие моменты в любом поперечном сечении K вычисляются в результате действия силы, расположенной на левой стороне поперечного сечения K-реакции и распределения нагрузки Tuq (x) X, полученной из подобия треугольника.- Никсы /\х г(*)=м — • И так оно и есть. Из этих уравнений видно, что участок Q очерчен вторичной параболой, а участок M-кубом. Чтобы построить их, мы вычисляем вертикальную ось в характерной точке! при x = о ок=;при x=я дь=——— ; ql6 21 В Q −0=0, т. е. Таким образом, участок Q имеет такую форму, как показано на рисунке. 73, а в сечении A (x=0) касательная участка Q
параллельна оси. В дальнейшем, В x=0MA-0;в x=I0.< 0. / 3 Если X=XO = дифференциал ДМ КЖ и / \ Т= — б — — — — — — — 2Т=, находим x0 из условия Q (x0)= — Zx0+6.02=0, 6.02 O =- з-м=2,01 м. Откуда ТС*м=-2.57 ТС * м. Тогда L1 (o)= [- — — ^’0P+ 6,02 (2,01 — 0 , 6 ) — Б]по полученным данным строим участок М. Например, где Q>0, момент M увеличивается, а где Q<0-уменьшается; график L4 в сечении E, сечении F и C M=0 в 5tc-M скачках. Было оценено, что любой интервал для Q M представляет собой представление диаграммы графика графика, когда есть возможность, что он доступен для такого. Достаточно рассчитать значения Q и M в характеристическом интервале. В этих случаях
можно рекомендовать следующую последовательность графиков: 1. Найдите опорные реакции (в случае консоли они не найдены). 2. На трамплинах и спусках обязательно идите по балке слева направо, постройте участок Q (для этого не нужно делать никаких записей). 3. Найдите характерное поперечное сечение балки. Характерными участками являются участки, в которых приложены сосредоточенные силы и моменты, и начинаются или заканчиваются распределенные нагрузки, а также участки, в которых Q исчезает. 604 участок вычислить характеристическое сечение значения M
и вертикальной оси, найденной для построения L1. Для консольной части балки следует руководствоваться общими характеристиками участка, при этом использовать известные для них участки (57 и 58). Пример 8. Постройте график Q и M шарнирной балки(рис. 75). Эта балка имеет четыре неизвестные составляющие реакции опоры-0= / Il, # A и Reиз-за отсутствия горизонтальных составляющих внешней нагрузки. Наличие промежуточного шарнира в точке С.、 Дополнительное выравнивание статики и превращение балки в статически определимый шарнир.
Смотрите также:
| Поперечные силы и моменты в сечениях балки | Построение эпюр для рам |
| Построение эпюр q и m в балках | Построение эпюр для криволинейных стержней |

