Оглавление:



Дифференциальные зависимости между внутренними силовыми факторами и нагрузкой в кривом брусе
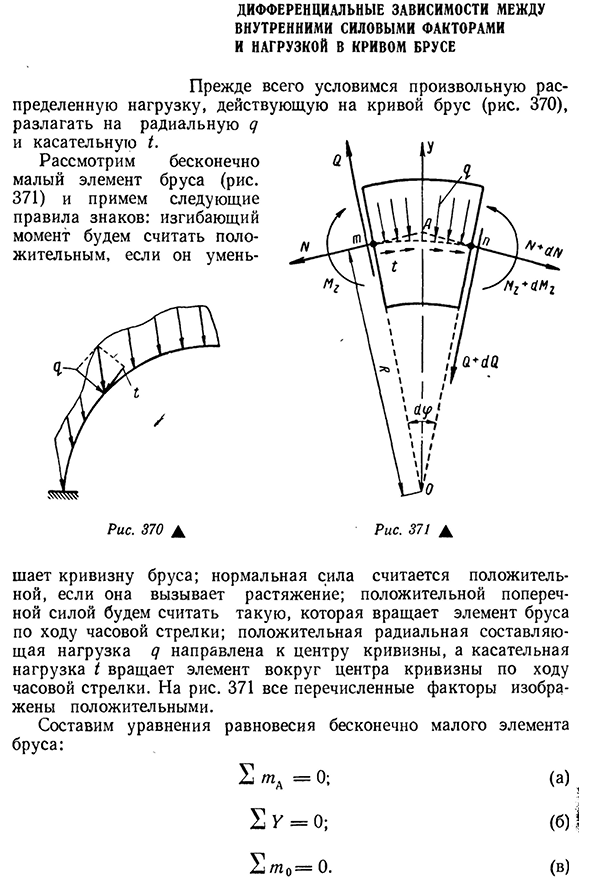
- Внутренние силы и факторы И нагрузка на криволинейную балку Сначала предположим любое распределение нагрузки, действующей на кривую балки (рис. 370), радиальная и касательная I. пожалуйста, свяжитесь с нами, если у вас есть какие-либо вопросы. Рассмотрим бесконечно малые элементы бара. 371)и принимаем следующие
правила маркировки: считаем положительным изгибающий момент, если он меньше Рис рис 370A. 371A Положительная радиальная составляющая нагрузки / 7 направлена к центру кривизны, а касательная нагрузка I вращает элемент по часовой
стрелке вокруг центра кривизны. Для риса. 371 указывает на все факторы. Составим Людмила Фирмаль
уравнение равновесия бесконечно малых элементов стержня: 4TC=0; (а)5У=0;(б) 2_t0=0. (В) 436 первое уравнение (а) имеет вид Есть TC=2 мы получаем Два. Литье Кроме того, учитывая, что длина TP дуги равна YZ, определяется вами—b / L1g4-/? FY’=0. Рейджен и у нас есть Ю. М. Г—(2=0. (14.1) (18 Второе выражение (b) записывается следующим образом:= — ^8—((? +ОД Ы О8+$SO8 -^ —(22У+Д з ш — ^ — =0. Учитывая малость дискуссии (19 1. (19 (19(19 Pop—1 ‘ 81P — — — 2 2 2’ Отбросив
высшие члены малости, мы имеем 4- + «+4=0- <14-2> Третье уравнение (b)2W b=(L^+A d/? — (Мг±с!Mg)+Mya-дать MYA+Mg=0 —- когда+я = О.(14.3)/? (18 (18)уравнения (14.1), (14.2) и(14.3) называются уравнениями Кирхгофа, если эти уравнения ставятся/? =OO, JB=(1x, первые два уравнения совпадают с ранее полученными уравнениями для прямого луча в§64. Третья формула для прямой балки представляет собой соотношение между силой продольного распределения
- нагрузки и вертикальной силой N (см.§6). Из уравнений 437(14.1)и (14.2) производная зависимость Mg и стержней кривой такая же, как и у прямых стержней, и зависимость между 7 может быть осложнена аддитивным действием вертикальной силы N. Эти ситуации следует учитывать при управлении строительством участка криволинейного
бруса. Рассмотрим конкретный случай. Пусть/? — рассмотрим круговой стержень только с радиальной нагрузкой, то есть sopz1 и/=O. тогда, если мы интегрируем уравнение (14.3), умноженное на C18、 — . (г) Здесь — — — — — — любая константа. Имея дифференцированное уравнение(14.1) и исключенное из него -, по уравнению (14.2) находим (18 a2m2=_ _ Ту нет. Я К’ Если выразить значение N из выражения (d), то оно выглядит так И что?2/?Два. А я-б и—- • / ?Два. (Д) d)
и заменить (ми) Должен ли я заменить независимую переменную, поставив 5=Людмила Фирмаль
знаменателе уравнение (e) принимает вид 4-й,= — «π’+C.(14.4) ASR2 Как только мы дифференцируемся, мы приходим к уравнению ■ ЛМГ_ _ ^2 взр(14.5) YSR3A SR YSR * Установите зависимость между изгибающим моментом и прочностью круглого стержня при рассеивании радиальной нагрузки. Это выражение используется позже в§125.
Смотрите также:
| Пример расчета тонкостенного стержня | Растяжение и сжатие кривого бруса |
| Расчет кривого бруса общие замечания | Чистый изгиб кривого бруса |

