Оглавление:






Дифференциальные зависимости между изгибающим моментом, поперечной силой и интенсивностью распределенной нагрузки
- Дифференциальная зависимость между поперечной силой и силой изгибающего момента, распределением нагрузки изгибающего момента M, поперечной силой Q и интенсивностью внешнего распределения нагрузки q, действующей на балку(фиг. 21.7 а) связан определенной зависимостью. В рамках действия распределенной нагрузки по двум секциям выбираются микроэлементы длины DZ. Левая и правая части этого элемента имеют положительные
изгибающие моменты и положительные боковые силы, которые увеличиваются с увеличением абсциссы z(рис. 21.7, 6). Когда изгибающий момент возникает в левом сечении элемента dz, правое сечение равно M — \ — dM. Получите те же добавочные и сдвиговые усилия. Сила распределенной нагрузки внутри бесконечно малого элемента dz, q, считается постоянной и положительной, если ее направление совпадает с положительным направлением оси операционного усилителя. Под действием всех приложенных сил элементы dz и вся балка находятся в равновесии.
Составим уравнение статического равновесия элемента dz в виде суммы моментов сил, Людмила Фирмаль
действующих на него относительно центра тяжести O среднего сечения: 1 1 1 2L40=м—(Л1+ДМ)+ — х элемент+ — — элемент+-&dQdz=0. 216ff) Отчет) Желание? Два. Рис 21.7 ДЗ Итак, первая производная функции изгибающего момента по длине балки равна поперечной силе. Запишем второе уравнение статического равновесия для элемента dz как сумму проекций на оси OU всех сил, действующих на этот элемент: 1, y=qdz — {- Q-q-dQ=0, где q=M/dz?. Таким образом, первая производная функции поперечной силы по длине балки равна интенсивности распределения нагрузки перпендикулярно ее
продольно ориентированной оси. Известно, что первая производная равна касательной угла a между осями и касательной кривой y=f (g). 1) тангенс угла наклона тангенса к эпюре изгибающего момента в сечении балки и оси эпюры равен поперечной силе в поперечном сечении; 2) сдвигающая сила; 4)в холостой части балки изгибающий момент эпюры изменяется по закону линейности, поперечная сила эпюры постоянна;5) 217эпюра м изменяется вдоль кривой, ее выпуклость совпадает с направлением внешней нагрузки. Если распределительная нагрузка имеет определенную интенсивность, то кривая м изменяется по закону вторичной параболы, а график Q изменяется линейно; 6)в сечении балки, с внешней стороны; 7)в
- сечении балки, где приложен внешний сосредоточенный изгибающий момент, величина внутреннего изгибающего момента резко изменяется по величине приложенного внешнего сосредоточенного изгибающего момента. Использование полученных выводов значительно упрощает построение фигур м и Q при изгибе балок, а также является удобным способом контроля правильности их построения. На основе этих зависимостей можно построить графики M и Q на балке без выполнения аналитического представления соответствующих сечений. Поясним, как вычислить величину изгибающего момента и силы сдвига в характерном сечении балки, чтобы она соответствовала границе земельного участка, а затем
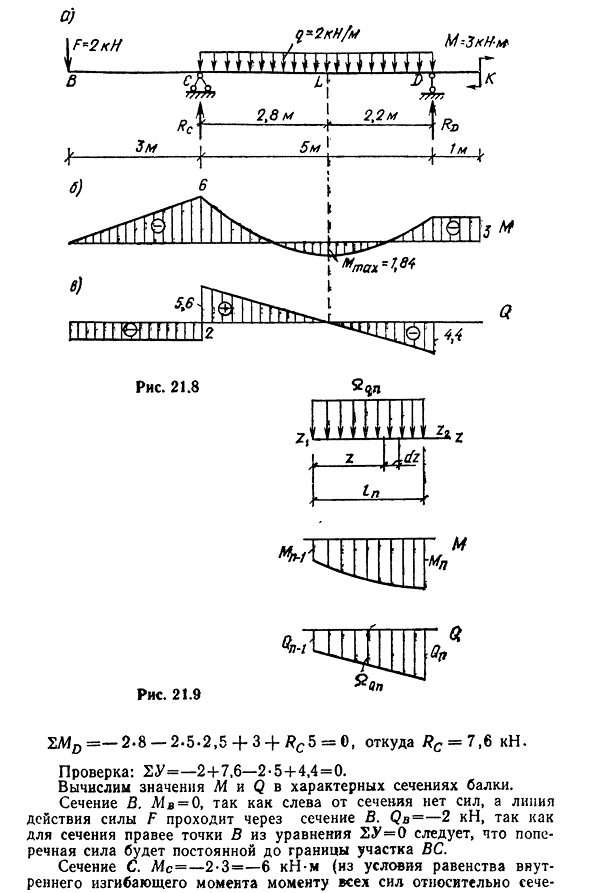
построить линии M и q, если на этом участке нет распределенной нагрузки. Например. Для балки (рис. 21.8,а)эпюры м и Q. Решение. Есть три секции этого луча: солнечная, CD и DK. Итак, в этих сечениях участок M изменяется по линейному закону, а участок Q имеет постоянное значение. Внешняя равномерно распределенная нагрузка приложена к сечению CD согласно закону графика Q-линейному, в своем диапазоне график M изменяется в соответствии с параболой квадрата. Из уравнений статического равновесия мы находим опорную реакцию: SZ-0; Yas=0; YMC= — 2-3 + 2-5″2,5 + 3 — I p5=0, где PD = 4,4 кн; 218а) У°2кн В C2kn/m M-ZKN-» W t h+C W I GT g — м2. 8м[2.2 м Р с \ ——— ——— +— 5—— |Яо. — .’————— М^4 Другие способы использования будут описаны позже. ►^гжп » ТТН Юг Ф М Х11? T7T7^?^IC / D / 4/ * Четыре. Рис 21,8 Зет М Рис 21,9 «Вт»» T’UJ — И
Четыре.» SMD= — 2-8 — 2″5-2,5 + 3 + /?И 5=примерно, где/?С=7,6 кн. Проверка:2U= -2+7,6—2-5 + Людмила Фирмаль
4,4=0. Вычислите значения M и Q для характерной части балки. Сечение B. MB=Q, где на левой стороне сечения отсутствует сила, а линия действия силы F является сечением B. Так как мы проходим через Qb= — 2kN, то сечение справа от точки B из уравнения 2U=0 Сечение С. МС= — 2-3= — 6кн-м(из эквивалентного условия внутреннего изгибающего момента момента всех сил на сечении- 219, Б, в левой части этого раздела. Потому что концентрированная эталонная реакция применяется к разделу C/?C=7,6, направленный снизу вверх, а затем график Q для прыжка, равный этой силе. Итак, в этом разделе мы вычисляем два значения поперечной силы: на левой стороне раздела Q^eB и на правой стороне раздела Q » P.= — 2kN; QJP= -2 + 7 ,6 = 5 ,6 кн. セクションD.MD— — 2-8-2-5-2,5+7,6 -5 = -3 кН-м в поперечном
сечении действует в пользу реакции/?d=4,4 кн. Найти два значения поперечной силы: слева от сечения QpeB=-2+7,6—2 -5 =-4,4 кн; и справа Q£p= -2+7,6—2-5+4,4=0. В крайнем сечении к приложен внешний изгибающий момент L4=3kN-m, который вызывает натяжение верхних волокон балки. Согласно принятым правилам знака, M считается отрицательным, поэтому L4x= — 3kN * m. График M и Q от расчетного значения(рис. 21.8, 6, б). В секции L секции CD боковая сила равна нулю, поэтому в этой секции изгибающий момент достигает максимального значения. Расположение участка L зависит от подобия треугольников участка Q на этом участке, а именно aL=5- 5,6/10=2,8 м. Максимальный изгибающий момент секции L: ML= — ;2″5,8 + 7,6-2,8 — 2-2,8-2,8/2 = 1,84 kN-M: может использоваться для визуализации разностных отношений между M и Q, а также для
построения и проверки правильности графиков M и Q. Рассмотрим любое сечение N пучка длиной 1 р в виде абсцессов Z\и G2(рис. 21.9). Запишите разностное отношение между M и Q, а именно dM!DZ=Q или dM=Qdz. Интегрируем левую и правую части этого выражения из-Mg^=j Qdz=в pre’p’P2 для отрезка n J tW=j Qdz. Здж Цзы * =&Qn или в системе(см. рис.. 21.9), мы получим АПН=Mn_i+-+QQn,где значение изгибающего момента в правой части МП-сайта N\МН-значение изгибающего момента в левой части у меня-сайте Н;Qqh- Таким образом, изменение величины изгибающего момента в сечении длиной 1 Р равно площади участка поперечной силы в этом сечении. Эта зависимость эффективна, если к этому участку не приложен внешний концентрированный изгибающий момент. FYA=<2n-1+ADP, где значение каждой из боковых сил в левом и правом сечениях qn
и qn-i-p\qqn-p графиков: диаграмма ощади распределила нагрузку на станции n. 220проверим участок М(рис. 21.8, 6). Рассчитан изгибающий момент в характерном сечении балки. Секция C: Mc=Mb+&qbc=0-2’3= — 6kN-m; секция L: Ml=M c+ & qc l= — 6 + 5.6-2,8/2= 1,84 kN-m; раздел D: Md=M l — \ — ^q^d= \ >84-4,4-2,2/2=-3 В разделе K: Mx=Md+QqD7<=-3+0= — 3kN-M. Результат расчета тот же-участок М построен правильно. Когда на балку воздействует большое количество внешних нагрузок, участки M и Q строятся отдельно от каждой нагрузки. Результаты суммируются алгебраически.
Смотрите также:
Решение задач по технической механике
| Допущения и ограничения, принятые в сопротивлении материалов | Изгиб прямого бруса. Основные понятия |
| Влияние способа закрепления концов стержня на критическую силу | Моменты инерции сечений |
Если вам потребуется заказать решение по технической механике вы всегда можете написать мне в whatsapp.

