Дифференциальные уравнения Л. Эйлера в естественной форме

Дифференциальные уравнения Л. Эйлера в естественной форме

Дифференциальные уравнения Л.  Эйлера в естественной форме. Уравнениями Эйлера в естественной форме называются диф­ ференциальные уравнения движения идеальной жидкости, выра­ женные в форме проекций на оси натурального триедра (на»ка­ сательную и главную нормаль к линии тока) (фиг. 8-5). Обозна­чая направление касательной через / и принимая во внимание, что проекция градиента давления на направление i равна (8 ‘28).

Смотрите также:

• Предмет гидравлика

Напомним, что движение материальной точки в пространстве задается тремя способами векторным, координатным и естественным. Людмила Фирмаль

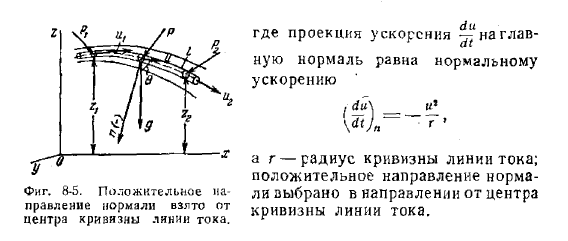
Аналогично для проекций на главную нормаль п получим: 120 Основные уравнения гидродинамики [гл. 8 где проекция ускорения ^ на глав­ ную нормаль равна нормальному ускорению / <*и __ г/5 а г — радиус кривизны линии тока; положительное направление норма­ ли выбрано в направлении от центра кривизны линии тока,

Смотрите также:

1. Дифференциальные уравнения движения идеальной жидкости (уравнения Л. Эйлера).
2. Уравнение Д. Бернулли для элементарной струйки идеальной капельной жидкости при неустановившемся и установившемся движении.

Дифференциальное уравнение в векторной форме, естественно, эквивалентно трем скалярным уравнениям. Людмила Фирмаль