Дифференциальные уравнения движения системы материальных точек

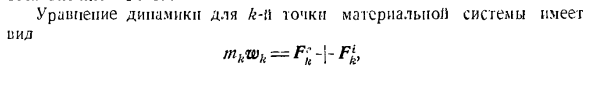
Дифференциальные уравнения движения системы материальных точек

• Дифференциальные уравнения движения системы масс В настоящей главе классификация внутренних (Р) и внешних (Fe) сил силы pa используется при рассмотрении системы массовых точек, в отличие от механики статики и массовых точек твердого тела, в которой сила делится на заранее заданные силы и силы реакции

сцепления. Внутренние силы — это силы взаимодействия между ключевыми точками, составляющими рассматриваемую систему. In кроме того, внутренние силы системы главный вектор V ’и главный момент m [равны пуле. V; = = = » — И)) = 0- И=> к \ •= » я Следует отметить, что в общих чертах система

Согласно принципу равенства действия и противодействия, внутренние силы существуют в pairs. Людмила Фирмаль

внутренних сил не сбалансирована, так как, несмотря на то, что эти условия выполняются, внутренние силы прикладываются к различным материальным точкам. Внешние силы-это те, которые применяются к критическим точкам рассматриваемой системы, от точек и тел, которые не являются частью этой и системы. Внешняя сила могов попадает в категорию внутренних сил, и наоборот. При

изменении конфигурации системы внутренние силы попадают в категорию внешних forces. So, учитывая систему, состоящую из 2 контактирующих шаров, давление первого шара nopofl и 2-го шара hierii является внутренней силой. Если рассматривать систему, состоящую из 1 первого шара, то давление 2-го шара относительно

• первого шара является внешней силой. уравнение динамики точки I-fi имеет важное значение]) в системе А = Н-1-Фе Где Feb-равнодействующая всех внешних сил, а Fj-равнодействующая всех внутренних сил, приложенных к материальной точке K-W. Ниже мы рассмотрим как систему, состоящую из конечного числа точек масс, так и систему тел с непрерывным распределением масс. Все теоремы сформулированы для системы важных точек, но система тел

может быть распределена без проблем. Дифференциальное уравнение k-ti движения точек масс в проекции на Декартовы координатные оси имеет вид: = Система из 3 уравнений. «Ля+=» В Дифференциальные уравнения движения системы из n материальных точек в проекции на ось декартовых координат описываются в виде: tpk = ’ F / tvi система 3 / / уравнение、 Где k = 1, 2, 3,…н. Поэтому для определения движения системы из n важных точек, составляющих систему, необходимо решить систему

чтобы найти постоянную, нужно дать Интеграл начальных условий движения. Людмила Фирмаль

обыкновенных 2-D уравнений 1N, которая содержит 3n неизвестных функций 3n независимой переменной t. 6 / /Имейте в виду, что внешние и внутренние силы могут зависеть как от времени, так и от расположения, скорости и ускорения точек в системе.

Решение такой задачи является сложным и трудоемким. Некоторые задачи динамики системы масс и массовых точек могут значительно упростить решение, применив так называемую общую теорему динамики.

Смотрите также:

Предмет теоретическая механика

Колебательное движение	Теорема о движении центра инерции системы материальных точек
Относительное движение	Теорема об изменении главного вектора количеств движения системы материальных точек