Оглавление:


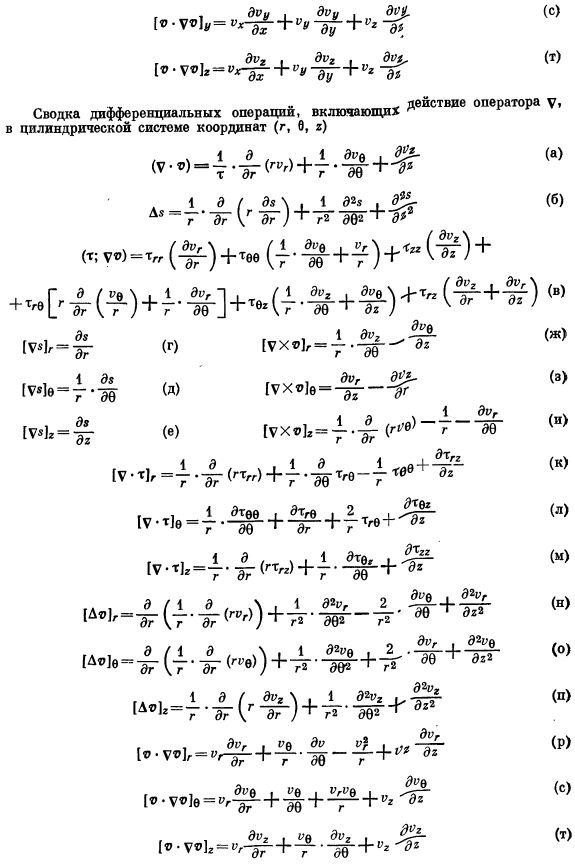




Дифференциальные операции в криволинейных координатах
- В предыдущем разделе компоненты вектора и тензора описывались в продольной криволинейной системе координат. Прямоугольный coordinates. In. В этом разделе 13, в криволинейных координатах * n&m & x*, нам даны выражения для различных дифференциальных операций, включая действие оператора «nabla». Следует подчеркнуть, что формула оператора V(A. 155) справедлива только в прямоугольной координате system. In другие системы координат, указанный оператор отличается. Это зависит от количества, на которое он действует, формы, которая зависит от скаляра, вектора или тензора, и типа продукта 3 ′ [продукт является типом TP. Он обозначается символами ( • ), (;) и (X)].
Оператор «nabla» является выражением (A. 136)и не следует правилам преобразования, определенным в». Ниже приведен обзор наиболее распространенных дифференциальных операций, которые записываются в прямоугольной, цилиндрической, сферической системе координат. Вышеуказанные отношения являются Получить, сформулировав соответствующую операцию в декартовых координатах с самого начала. То есть мы прорезаем их через дифференциал по координатам x, y, a(или по координатам Xz xa, xz).Далее рассмотрим Формулы (A. 137) и(A. 142), компоненты вектора и тензора могут быть представлены в декартовых координатах относительно компонентов любой криволинейной системы.
Шух показал, что переход к обыкновенным дифференциальным уравнениям возможен не только для плоской пластины, но и для ряда других геометрий поверхности. Людмила Фирмаль
Применение правил расчета Частные производные позволяют перейти от производных x, y и s к производным соответствующих криволинейных координат. Процедура получения формулы дифференцирования Операция в криволинейных координатах показана в Примере а-4.Эта процедура очень проста, но несколько утомительна. Выражение для записанной операции разности Для любой декартовой системы через соответствующий коэффициент хромоты L/, вы можете найти его в справочной математической литературе| 3-o].
- Обобщение производных операций, связанных с действием оператора V в декартовых координатах (x, y, d)** Операции, связанные с преобразованием Ковариантных и контрастных тензоров, можно систематизировать с помощью символа Кристоффера(см., например, монографии [1.21]. Ниже тензорные операции применяются только к симметричным тензорам.
Оператор V действие, краткое описание дифференциальных операций, в том числе Цилиндрическая система координат (g, 0, g) Сводка дифференциальных операций, включая действия оператора в сферических системах координат (r, 0, f) Найди а-4.Вывод формулы нескольких дифференциальных операций в цилиндрических координатах. Описывает выражение продукта (y-V) и компонент r [y-t]продукта Цилиндрическая система координат, rpe m, является 2-м рангом симметричного тензора. Решение, а) в декартовых координатах скалярное произведение (y * p) описывается как: Формула справа от этой зависимости (A. 127) — (A. 129) для замены определенных компонентов скорости у и p2 на Формулу.
В этих решениях характеристики, включая плотность, рассматривались как (постоянные во всех членах, за исключением последнего в уравнении движения, где имеется разность между локальной плотностью в пограничном слое и плотностью снаружи (пограничного слоя при одном и том же х. Людмила Фирмаль
И затем Здесь, используя реляционное выражение, частные производные (A. 146) Здесь мы подставляем вместо них и помещаем их формулы в py = «R cos0-p9 8 * n 0 и» ^ дифференциал цилиндрических координат r0 x и y(A. It можно легко найти из соотношения (110) и (AL11). Формула (A. 146)правая формула(A. 147) и(A. 148) заменяет эти производные. И затем… При выполнении всех этих дифференциальных операций и соответствующей репозиции элементов получается следующее конечное выражение: Дженни. Он появляется на странице 671. b) формула (A. 124) из、 Вектор декартовых координат[V -?Компонент [] определяется соотношением (a.
Если эти компоненты находятся в Формуле (A. 155), если вы явно подставлены справа, вы увидите следующее: Здесь в качестве коэффициента 1^, используя сумму, образующую матрицу, используется отношение (А. 142) Матрица (а) 157), формула (А. 127)-(А. 129).Поэтому соотношение (А. 142)позволяет описать совокупность взаимосвязанных уравнений: Ингредиенты для прямого тензора t Уголь и цилиндрическая система координат: После нахождения ряда сокращений необходимо отнести эти отношения к праву равенства А.
Смотрите также:
| Интегральные теоремы для векторов и тензоров | Температурное поле и поле теплового потока |
| Компоненты векторов и тензоров в криволинейных координатах | Вывод дифференциального уравнения Фурье |

