Оглавление:


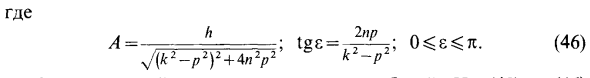

Дифференциальное уравнение вынужденных колебаний и его интегрирование
- Чтобы прояснить влияние линейного сопротивления на вынужденную вибрацию, рассмотрим наиболее распространенный случай, когда обобщенная сила Q состоит из трех сил. Потенциал Qn = —dP / dq— —eq, линейное сопротивление b (φ, = −dF / da = — == Hsin (pz + 8). Подставляя это значение обобщенной силы Q = Q «+ Q’t + QB в уравнение Лагранжа (1), aq + \ uj + cq = Hsm (pi + 5). Разделим обе части уравнения на π и введем обозначение k2 = c / a, 2n = c / a, h = Hja. Где A: круговая частота естественной вибрации.
Коэффициент демпфирования, а h относительная амплитуда возмущающей силы. Окончательный вид дифференциального уравнения: q + 2nq + k2q = hs \ n (pt-y8). (44) Линейное дифференциальное уравнение получается с постоянным фактором вынужденной вибрации, который учитывает линейное сопротивление. Поскольку это неравномерное уравнение, решение состоит из двух частей. qx — общее решение для равномерного уравнения. q2 является частным решением неоднородного уравнения. Общее решение однородного уравнения удовлетворяет уравнению для собственных колебаний с линейным сопротивлением.
Но для выявления сил, действие которых испытывает материальная точка, выберем ее собственную систему отсчета, по отношению к которой ее относительные скорость и ускорение равны нулю, т. Людмила Фирмаль
Таким образом, это движение не может быть вибрацией, но называется его собственным движением или вибрацией. Частное решение неоднородного уравнения q2 называется вынужденным колебанием. Общее движение системы характеризуется обобщенной координатой q, равной сумме qt и q2, где q = qt + q2 величина q называется общим вынужденным движением (или вынужденной вибрацией). Общее решение qt для однородного дифференциального уравнения q1 + 2nql + k2qi = 0 может быть выражено в одной из следующих трех форм в зависимости от соотношения между величинами n и k. n k, ql = e «‘(cie’ ^ r2 ‘+ C2 .
В любом из этих случаев qt стремится к нулю с течением времени, то есть затухает из-за наличия коэффициентов e ~ q. Если коэффициент демпфирования мал (n A) движение не будет колебаться, поскольку затухание очень велико. Следовательно, если через некоторое время возникает линейное сопротивление, суммарное вынужденное движение <y немного отличается от вынужденной вибрации, 9 = 92- Конкретное решение q2 в уравнении (44) должно быть найдено в виде q2 = A sin (pf-i-5 — s). Константы А и е определяются из следующих условий: Если q2 присвоено уравнению (44), оно становится тождественным. Для этого вычислите производную от q2. q2 = Ap cos (pt + 8 — s); q2 = -Ap2 sin (pt + 5 — r).
Преобразуйте правую часть выражения (44), чтобы включить косинус и синус того же аргумента, что и функция q2. Чтобы сделать это, сложите и вычтите значение е в нужную фазу, чтобы выявить знак суммы. x sin (pt + 8) = h sin [(p / + 8 — s) + s] = асин, потому что (pt + 6 — s) + аксоссин (p <+ 8 — s). Имея это в виду, мы подставляем значение q2 и его производную в уравнение (44) и собираем члены sin (pt + 8 — s) и cos (p / + 8 — s). Получить личность [A (k2 — p2) —Acoss] sin (pt + b — s) + + [2Lir — Asins] cos (pz + 8 — s) sO.
- Поскольку синус и косинус переменных аргументов не равны нулю одновременно, тождество может быть удовлетворено только в том случае, если каждая константа в квадратных скобках равна нулю. A (k2-p2) = глюкоза; 2Anp = hsim. Из этих уравнений определяются амплитуда и сдвиг фазы s вынужденной вибрации А. A- Формула греха показывает, что грех является положительным значением. Следовательно, значение r находится между маслами. Таким образом, для определения s достаточно использовать выражение только для одной тригонометрической функции, например, tgs. Окончательная форма выражения вынужденной вибрации составляет 92 = / фсин (pr + 8-с), (45) где A = ; tge = 2np; O ^ e ^ l. V ‘( 2-P2) 2 + 4 ”2P2 k -P (46)
Окончательный вид дифференциального уравнения: q + 2nq + k2q = hs \ n (pt-y8). (44) Линейное дифференциальное уравнение получается с постоянным фактором вынужденной вибрации, который учитывает линейное сопротивление. Поскольку это неравномерное уравнение, решение состоит из двух частей. qx — общее решение для равномерного уравнения. q2 является частным решением неоднородного уравнения. Общее решение однородного уравнения удовлетворяет уравнению для собственных колебаний с линейным сопротивлением.
В течение фазы восстановления т2 материальная точка от момента наибольшей деформации до ее отделения от поверхности частично восстанавливает свою первоначальную форму при упругом ударе. Людмила Фирмаль
Таким образом, это движение не может быть вибрацией, но называется его собственным движением или вибрацией. Частное решение неоднородного уравнения q2 называется вынужденным колебанием. Общее движение системы характеризуется обобщенной координатой q, равной сумме qt и q2, где q = qt + q2 величина q называется общим вынужденным движением (или вынужденной вибрацией). Общее решение qt для однородного дифференциального уравнения q1 + 2nql + k2qi = 0 может быть выражено в одной из следующих трех форм в зависимости от соотношения между величинами n и k. n k, ql = e «‘(cie’ ^ r2 ‘+ C2e ~ В любом из этих случаев qt стремится к нулю с течением времени, то есть затухает из-за наличия коэффициентов e ~ q.
Если коэффициент демпфирования мал (n A) движение не будет колебаться, поскольку затухание очень велико. Следовательно, если через некоторое время возникает линейное сопротивление, суммарное вынужденное движение <y немного отличается от вынужденной вибрации, 9 = 92- Конкретное решение q2 в уравнении (44) должно быть найдено в виде q2 = A sin (pf-i-5 — s). Константы А и е определяются из следующих условий: Если q2 присвоено уравнению (44), оно становится тождественным.
Для этого вычислите производную от q2. q2 = Ap cos (pt + 8 — s); q2 = -Ap2 sin (pt + 5 — r). Преобразуйте правую часть выражения (44), чтобы включить косинус и синус того же аргумента, что и функция q2. Чтобы сделать это, сложите и вычтите значение е в нужную фазу, чтобы выявить знак суммы. x sin (pt + 8) = h sin [(p / + 8 — s) + s] = асин, потому что (pt + 6 — s) + аксоссин (p <+ 8 — s). Имея это в виду, мы подставляем значение q2 и его производную в уравнение (44) и собираем члены sin (pt + 8 — s) и cos (p / + 8 — s). Получить личность [A (k2 — p2) —Acoss] sin (pt + b — s) + + [2Lir — Asins] cos (pz + 8 — s) sO.
Поскольку синус и косинус переменных аргументов не равны нулю одновременно, тождество может быть удовлетворено только в том случае, если каждая константа в квадратных скобках равна нулю. A (k2-p2) = глюкоза; 2Anp = hsim. Из этих уравнений определяются амплитуда и сдвиг фазы s вынужденной вибрации А. A- Формула греха показывает, что грех является положительным значением. Следовательно, значение r находится между маслами. Таким образом, для определения s достаточно использовать выражение только для одной тригонометрической функции, например, tgs. Окончательная форма выражения вынужденной вибрации составляет 92 = / фсин (pr + 8-с), (45) где A = ; tge = 2np; O ^ e ^ l. V ‘( 2-P2) 2 + 4 ”2P2 k -P (46).
Смотрите также:
Задачи по теоретической механике
| Затухающие колебания | Основные свойства вынужденных колебаний |
| Затухающие движения | Исследование вынужденных колебаний |

