Дифференциальное уравнение установившегося неравномерного плавно изменяющегося движения грунтовых вод при линейном законе фильтрации.

Дифференциальное уравнение установившегося неравномерного плавно изменяющегося движения грунтовых вод при линейном законе фильтрации.

Дифференциальное уравнение установившегося неравномерного плавно изменяющегося движения грунтовых вод при линейном законе фильтрации. Такие движения чаще всего наблюдаются в виде безнапорных движений со свободной поверхностью(рис. 27.4).Для него справедлива формула Дюпюи (27.12). как уже указывалось, игнорируйте скоростной напор во всех точках сечения З = р + п / рд = с + ч、 Где а-высота расположения ограничительной грани на опорной плоскости 0-0 рассматриваемого сечения. to-глубина потока в этом разделе.

Гидравлический градиент может быть представлен в виде Где 1 = Ла / ки(как я увеличивается, высота уменьшается).Затем из (27.12) У = К(1-s1Sh1). (27.17). Людмила Фирмаль

• Уравнение течения для этого типа движения грунтовых вод выражается в виде φ=ω и= K х>(} Ык! У1). (27.18） К0 = сопи! В случае равномерного движения и yk1y1 = о 2 = k (o01. Если умножить обе стороны формулы (27.18) на произвольное положительное смещение Γ, то: (Ив = ГХ((-(СГ /(второй). 2′ = ksh ’показывает скорость потока через при условии, что биоканальное поперечное сечение склона равно I’.Этот расход в каждом живом разделе отличается. У нас есть Используя уравнение (27.19), анализируется форма кривой свободной поверхности потока грунтовых вод на любом поперечном сечении.

• Для учета плоских задач ограничьте его прямоугольными формами поперечного сечения и перемещениями в каналах, имеющих достаточную ширину. Для плоских задач 7 = kk(1-cksh). (27.18 а） Учитывая, что определенное потребление может быть выражено в соответствии с (27.15), для прямого градиента (1> 0 (27.19 а） Или с11 = М1-..(27.20） *(Л-А0） Обратный градиент (*0)вызывает равномерное движение потока вдоль запорной пластины с градиентом V_g, учитывающим глубину нормали k’0.И затем… Уравнение (27.20)-после интегрирования (27.206) вы получаете выражение, определяющее длину кривой поверхности свободной формы. Рассмотрим кривую подавления, которая является возможной формой кривой свободной поверхности.

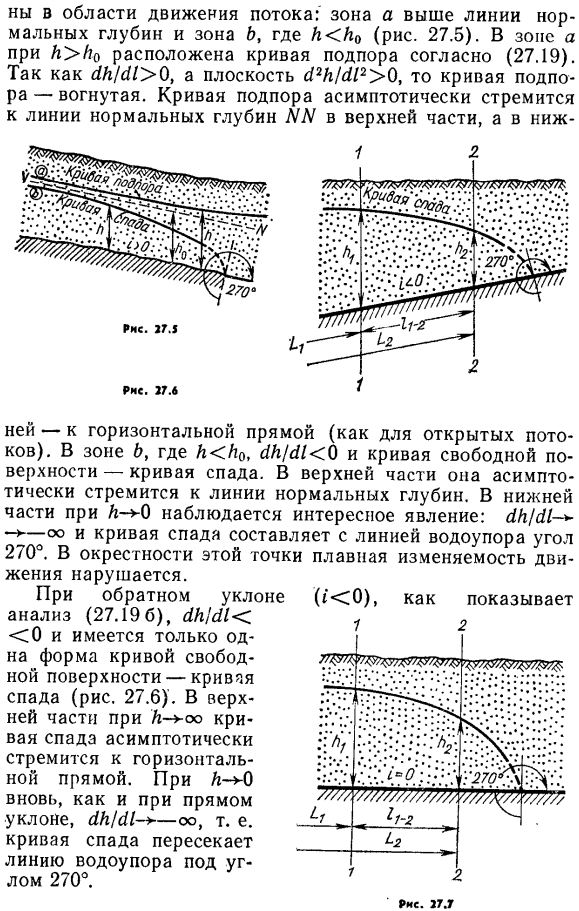
В ограничительном прямом наклоне (I> 0), 2 Они находятся в зоне движения потока: зона A и зона b k0 выше нормальной линии глубины (рис. 27.5).в зоне a при k> ko имеется кривая подпора согласно (27.19). Кривая подпора вогнута, потому что Нг / с11 > 0 и 平1212 / с112 > 0. Людмила Фирмаль

• Кривой подпора, как правило, носят асимптотический к нормальной глубины линии НН в верхней и нижней части. это до горизонта (в случае открытого течения). в зоне b, кк0, ik / BK и кривая свободной поверхности уменьшаются curves. In в верхней части наблюдается тенденция к асимптотике к линии нормали depth. At внизу A»-0, мы видим интересное явление: Лк / и * —» ОО, и кривая спуска образует угол 270 ° с ограничивающей линией. Вблизи этой точки происходит нарушение плавной изменчивости движений. Анализ обратного смещения(27.19 6), yk!(И 0, а кривая свободной поверхности имеет только 1 вид-приведенную кривую (рис. 27.6). в верхней части, как k * oo, кривая распада асимптотически горизонтальна. Опять же при k * 0, Lk / M * как и прямой наклон oo, то есть кривая уменьшения пересекает ограничивающую линию под углом 270°. 547. 35. Градиент равен нулю(27.19 с) 1к / с11.Если формат кривой свободной поверхности равен 0, ТО 1 является приведенной кривой (рис.27.7).

Смотрите также:

Решение задач по гидравлике

Возможно эти страницы вам будут полезны:

1. Коэффициент фильтрации.
2. Особенности плавно и резко изменяющегося движения грунтовых вод.
3. Расчет кривых подпора и спада при ламинарной фильтрации.
4. Приток к вертикальным скважинам (колодцам).