Оглавление:



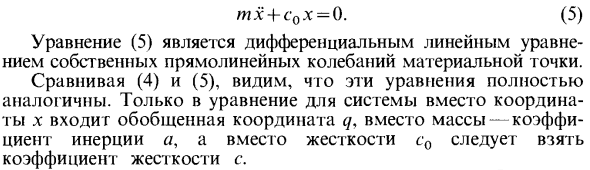

Дифференциальное уравнение собственных линейных колебаний системы
- Чтобы вывести линейное уравнение малых собственных колебаний из уравнения Лагранжа (1), кинетическая и потенциальная энергии должны быть последовательно расширены вблизи положения равновесия системы. Предположим, что система голономных, идеальных, неосвобожденных и фиксированных связей состоит из N точек и движется вблизи положения равновесия. Ее кинетическая энергия При сделанных предположениях о совместной стационарности радиус-вектор r * каждой точки в системе зависит от времени только через обобщенную координату q.
Следовательно, rk = — ^ q. Подставляя этот гк в выражение кинетической энергии, Как и в случае с gk, величина A может зависеть только от q, а не от q. Когда A (q) расширяется вблизи q = 0 степенного ряда, Далее индекс 0 означает, что соответствующее значение вычисляется с q = 0. Чтобы получить кинетическую энергию в терминах квадратичного и более низкого членов для q и q, достаточно получить только постоянное значение Ao из разложения A (</), представленного a. Принимая во внимание другие члены из разложения A (q), отображаются третьи и более высокие члены.
Следовательно, в опыте Фуко маятник описывает эллипс в отрицательном направлении вращений вокруг оси Ог, в то время как сам эллипс вращается вокруг той же оси в положительном направлении. Людмила Фирмаль
Следовательно, выражение кинетической энергии путем отклонения третьего и более высоких членов можно выразить следующим образом. (2) Положительная постоянная а называется коэффициентом инерции. Обычно коэффициент инерции равен массе или моменту инерции. Потенциальная энергия системы P для стационарного силового поля и стационарной связи является функцией только обобщенной координаты q. Расширяясь до степенного ряда вблизи q = 0, получим Потенциальная энергия Po в равновесии при q = 0 принимается равной нулю.
Значение [dP / dts) 0 является значением обобщенной силы Q в положении равновесия системы и равно нулю. Предположим, что в равновесии потенциальная энергия минимальна. Это является достаточным условием устойчивости положения равновесия системы. В этом случае Значение OFm (d2P / dd2) 0 положительное, t «* ‘T x указывает, что константа (- • ——- «Они определяются коэффициентом жесткости Или просто жесткий. Рисунок, но, следовательно, уничтожить слабых Есть заказ более третичный n (q) = 1 / 2cq2- (3).
- Система, в которой кинетическая энергия и потенциальная энергия точно представлены в соответствии с уравнениями (2) и (3) без отбрасывания членов более высокого порядка, называется линейной. Для них вся математическая система такая же, как и система, которая совершает небольшие колебания, но колебания линейной системы являются произвольными и необязательно малыми. Далее рассматриваются линейные колебания, включая небольшие колебания. На основании (2) и (3) вы получите.
Подстановка этих производных значений в уравнение Лагранжа (1) дает следующее дифференциальное уравнение для небольшой собственной вибрации системы с одной степенью свободы. aq + cq = 0. (4) Если третий и более высокий члены учитываются при расширении кинетической энергии и потенциальной энергии, второй и более высокий члены появляются в уравнении (4), и дифференциальное уравнение становится нелинейным. Получите дифференциальное уравнение для линейной вибрации точки массы, которая не обязательно мала. Масса M массой m движется линейно вдоль оси Ox под действием силы F.
Будем считать, что после присоединения точки становятся точками рассматриваемого тела, после отделения точки перестают взаимодействовать с телом и исключаются из дальнейшего рассмотрения. Людмила Фирмаль
Сила F линейно зависит от расстояния точки от положения равновесия O и стремится вернуть точку в положение равновесия (рис. 110). Поместите начало расстояния x в положение равновесия (точка O). Сила F направлена на начало расстояния (точка O). На данный момент он равен нулю. Проекция на ось О Fx = -cox, Где постоянная с0 — жесткость. Сила F в этом случае называется линейной восстанавливающей силой. Упругая сила согласно закону Крюка — это линейная восстанавливающая сила.
Подстановка значений линейной восстанавливающей силы в дифференциальное уравнение для линейного движения точек и преобразование всех членов в часть уравнения дает: mx + cox = 0. (5) Уравнение (5) представляет собой линейное дифференциальное уравнение естественной линейной вибрации точки массы. Сравнивая (4) и (5), вы можете видеть, что эти уравнения полностью аналогичны. Только в системных уравнениях вместо координаты x обобщенной координате q необходимо ввести коэффициент инерции a вместо массы и получить коэффициент c жесткости вместо жесткости c0.
Смотрите также:
Задачи по теоретической механике

