Оглавление:




Дифференциальное уравнение оси изогнутой балки, лежащей на сплошном упругом основании
- Дифференциальные уравнения оси Изогнутые балки, лежащие на твердом теле упругое основание В инженерной практике мы часто сталкиваемся с балками, которые находятся на сплошном упругом основании. Такими балками можно считать железнодорожные пути
шпалы на конвейерах 325фундаменты здания на основе грунта, фундамента плотины и др. Кроме того, такие балки также являются рельсовыми с бесконечно большим количеством опор,и расстояние между ними невелико по сравнению с длиной.
Расчет балки на упругом основании не может быть осуществлен с использованием Людмила Фирмаль
уравнений статики. Эта задача не определена статически. Уравнения статики позволяют найти только суммарную реакцию от основания, а не определить закон распределения реакций по длине пучка. Величина реакции в каждой точке зависит от отклонения луча, а отклонение луча зависит от реакции от основания. Для решения этой задачи обычно принимается гипотеза о величине реакции на
оседание основания. В качестве одной из наиболее распространенных гипотез, л л ь н о й з а б и с т и М ф д У Р Е К К И Й с К и й л ь н о й С К И Й с Л О В а н о й С К И Й с К и й Эта гипотеза о характеристиках почвы была впервые предложена акад. Н. И. сыр-бор из-1801 и его применение к балкам на упругом основании вел профессор Э. Он широко используется Винклер. В последнее время было выдвинуто
- несколько новых гипотез. Таким образом, одна из них состоит из двумерного упругого основания, отдельной пружины, соединенной нитью в неупругом горизонтальном положении у верхнего края, и ее концов так называемой упругой полупространственной гипотезы.И широко принят. Однако решение инженерных задач методами, основанными на этих гипотезах, все еще очень трудоемко. Рассмотрим расчет балки на основе упругости по гипотезе Фусса-
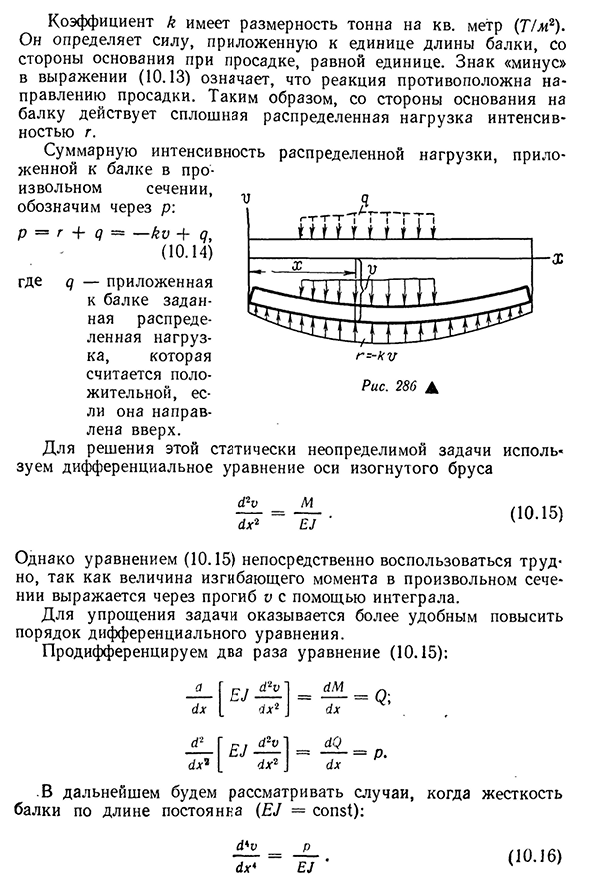
Винклера. Для риса. На рис. 286 показана картина деформации балки от внешней нагрузки, распределенной по любому конусу. Предполагается, что реакция от основания в каждой точке пропорциональна отклонению Г=-Ко(10.13) Куда? K=K\g-базовая реакция на единицу длины пучка, Т!M\V-просадка основания^, m\K ‘ — коэффициент пропорциональности, называемый
коэффициентом гибкости основания, или отношением ложа H/mg. Это соотношение Людмила Фирмаль
представляет собой сопротивление основания на 1 м2 в случае просадки, ширину балки B-кровати. В 326coefficient K имеет размеры тонн на квадратный метр(77м2). Он определяет силу, приложенную к единице длины балки от нижней части просадки равной единице. Знак минус (10.13)в выражении означает, что реакция противоположна направлению просадки. Таким образом, непрерывное распределение нагрузки g-интенсивности действует на балку со стороны основания. Общая сила распределительной
нагрузки, приложенной к балке в любом сечении, равна p: p=g4-d—Ki4-7, (10.14) Где d-распределительная нагрузка, приданная балке, и если она направлена вверх, то считается положительной. Для решения этой статически неопределенной задачи используются дифференциальные уравнения криволинейной оси пучка Сайт a2u (1х2 М Е } (10.15)) Однако величина изгибающего момента в любом поперечном сечении выражается через прогиб V с помощью интеграла, поэтому формулу (10.15) трудно использовать непосредственно. Для упрощения задачи удобнее увеличить порядок дифференциальных уравнений. Дифференциал по двойному
уравнению(10.15)): Но Да Е} с!2У а Х2 (И2 s1x* E1 y2u <1х2 М<1х 。В дальнейшем мы будем рассматривать, является ли жесткость длины балки постоянной(E7-sopz1): По№ Д. Ч.* п Е} (10.16) Из 327поставив(10.14)в (10.16)значение интенсивности распределенной нагрузки, получим _- Ки+9ач*е] Или *1) Девять. Четыре. АхЕ^Е^ Позвольте мне ввести обозначение: К Е^ =4÷4; g V нет. (10.17)) (10.18) Значение P имеет размеры (Длина-м\см). Тогда дифференциальное
уравнение изгиба (10.17) принимает вид а4і б/Х4 Д Е} (10.19) Уравнение (10.19) особенно полезно использовать, если d=0. Если нагрузка линейно зависит от x, то это уравнение лучше представить в другом виде. Дифференцируем выражение (10.19)дважды,чтобы умножить его на первое E.: Ми^ АВ1>yh6 +4º4E / ~0х‘ Или другие (EM’)™+4p4 (EM’)=9″. Когда мы думаем о»EM» =M、 а * м а*4-4≤4М=д». (10.20 утра)) Оба дифференциальных уравнения эквивалентны и могут быть использованы для решения практических задач.
Смотрите также:

