Оглавление:



Дифференциальное уравнение изогнутой оси
- Дифференциальное уравнение для оси отклонения. Чтобы получить y как функцию от X, необходимо установить зависимость величины и материала деформации балки от внешних сил, изгибающих ее. Мы уже получили эту зависимость от 78. Мы используем формулу,
полученную с учетом чистого изгиба (13.10). Распространяя его на общий случай изгиба, то есть игнорируя влияние боковых сил на деформацию балки, можно записать 1_M (х)р (х) — СЗ’ Где p (x) — радиус кривизны участка криволинейной оси балки между
двумя соседними участками на расстоянии x от начала координат, и/или(x) Людмила Фирмаль
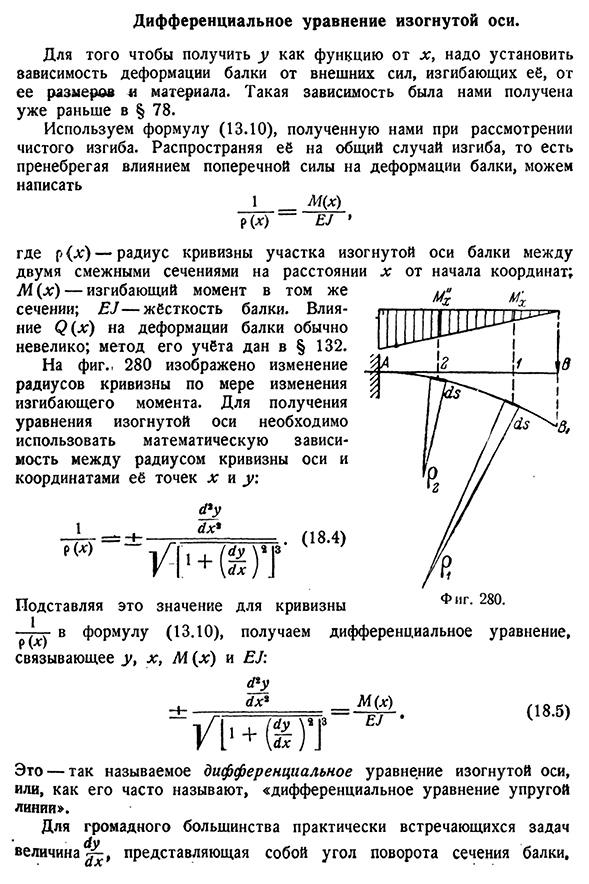
влияние f (x) на деформацию одного и того же участка балки обычно невелико; способ его заполнения приведен в § 132. Как использовать при изменении изгибающего момента,>280 указывает на изменение радиуса кривизны. Чтобы получить уравнение для оси кривой, необходимо использовать плоскость между координатами Математическая радиус радиус кривизны в точках X и y\ Зависимая ось и Один. П(*) Д * Г ДХ* (18.4) МГН Подставляя значение этой
кривизны в g уравнения (13.10) , получаем дифференциальное уравнение P W Y t x, M (x), EJ: Ru rfx8M (x)в сочетании с G•(18.5)) Это так называемое дифференциальное уравнение оси кривой, или, как его часто называют,»дифференциальное уравнение упругих линий». Для большинства задач, возникающих на практике, представлен угол
- поворота сечения балки 354 аналитическими методами определения деформации[гл. XVIII Фигура. Двести восемьдесят один И уравнение (18.5) упрощается: Это уравнение называется приближенным дифференциальным уравнением для криволинейной оси балки. Правило знака изгибающего момента устанавливается независимо от направления координатных осей (как известно, вторая производная равна 281), при котором вогнутая часть кривой
поворачивается в сторону положительной оси Y. Таким образом, знак изгибающего момента M(x) не зависит от положения осей координат. В направлении оси Y вверх знак a должен оставаться в выражении (18.6). В нижней части, знак-. Условимся в дальнейшем сделать ось Y всегда вверх и записать дифференциальное уравнение (18.6) в виде E J-g — =7M (x). (18.7) в то же время момент еще поставлен Правила. Уравнение (18.7) должно быть интегрировано, чтобы получить уравнение кривой оси уравнения отклонения y=/(x). Итак, когда вы интегрируете, E J — ^=J M (x) d x+C; Если вы интегрируете второй раз, вы получите EJy=Y dx Y M (x) dx CX D. Таким образом, мы получили уравнение угла поворота: е= ’ е ’ =4Р[дж дж м (х) р F х + с](1 8-8 ) И уравнение отклонения: Метки изгиба D X(x) d x —
| — x — / — D j. (18.9) эти уравнения включают интегральные константы C Людмила Фирмаль
и D. Порядок вычисления этих констант показан в Примере.§ 1 1 0] Формула изогнутой оси балки, зажатой омами 3 5 5 Прежде чем перейти к фактическому примеру, необходимо еще раз подчеркнуть, что выражение (18.7) является приблизительным значением.} погрешность игнорирования величины сравнения с единицей заключается в том, что деформация балки не удовлетворяется, а угол сечения балки не равен квадрату угла ее величины по сравнению с величиной) Такие случаи могут быть при исследовании деформаций при изгибе тонких пружин, тонкой фанеры, в общем случае гибких балок.
Смотрите также:

