Оглавление:
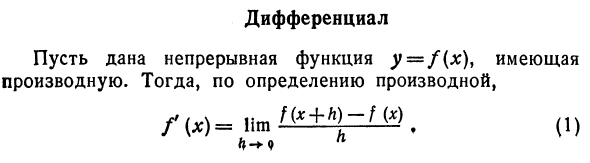



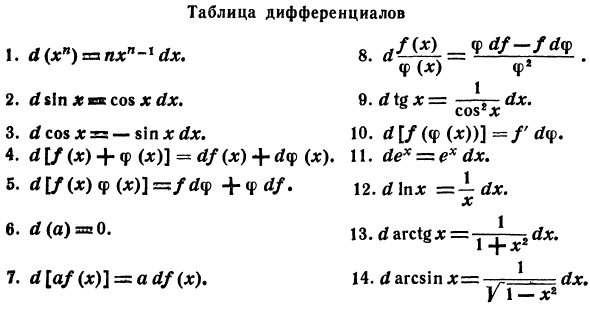

Дифференциал
- Дифференцированный Сделать непрерывную функцию Производные финансовые инструменты. Затем, определяя производную, / »- \ Imnx + h) -f (x). (1) Следовательно, инвертирование символа ограничения справа вызовет ошибку. Его значение зависит от х и А. Эта ошибка обозначена как (n:, A). Тогда вместо уравнения (1) / () + Α (, k) = f * + k) -, {*. (2) Об ошибке a (l;, l) Лима (л:, А) = 0. (3) Это основано на уравнении (1). Следовательно, ошибка a (x :, A) бесконечно мала по отношению к приращению независимой переменной A.
Умножение A на обе стороны (2) уравнения: f ‘(x) h + a (x, h) h = f (x + h) -f (x), или по = f (x + h) —f (x) = f (x) h + a (x, K) A. (4) Давайте оценим порядок малости этих членов. Нш® = / (4 ч- «о р lim a (x, h) h = um a ^ h) = QeЛоЛhо Очевидно, что первое слагаемое f ‘(x 🙂 h (если f’ (x 🙂 Φ0) имеет тот же порядок, что и h, т. Е.
С левой стороны уравнения (4) находится приращение функции Du, а с правой стороны — два слагаемых f ‘(x) A и a (jt, A) A. Людмила Фирмаль
Линейно относительно A, а второе слагаемое a (x, A) A бесконечно мало Это высший порядок по ч. Из уравнения (4) мы видим, что приращение функции равно / ‘(x) h, вплоть до наименьшего высокого порядка. Это выражение называется функцией дифференцирования. Определенная производная является частью приращения функции D y, которая является линейной по отношению к h. Таким образом, производная функции равна произведению производной на приращение независимой переменной. Производная функции dy или df (x), поэтому dy = df (x) = f ′ (x) h. (5)
Для симметрии записи было введено независимое определение непостоянной разности. Определение Производной независимой переменной является ее приращение. Производная независимой переменной обозначается через dx}, поэтому dx = h = Ax. (6) Операция поиска производной называется дифференцированием. Пример 1. Найти производную функции y = * = sinx. Поскольку (sin x) ‘= cosx, dy = d sin x = cos l: -L = cosxdx. Пример 2. Если η: = 2 и dx = h = 0.1, вычислим производную функции y = x . (X’Y = 3x *, тогда dy = 3l; * dx, где значение 2 заменено на x, а значение 0.1 заменено на dx, dy «3-21.0,1 = 1,2. п-0,1
- Из определения производной функции вы можете видеть, что производная функции одной переменной является функцией двух переменных. , Из уравнений (5) и (6) f ′ (x) = y = Следовательно, производная равна отношению производной функции к производной независимой переменной. Теперь мы будем использовать как символ (), так и отношение производной, чтобы указать дифференцирование.Дифференцирующий стол V FW F 2.d% \ nx * x cosxdx. 9.d tg x = 3. rfcos * =: -s \ nxdx. 10. rf [/ (φ (■ *))] = / ‘dy. 4. d [f (x) + (x). 11. de * = ex dx. 5. d [f (x)
- + df. \ 2.d \ nx — dx. х 6. = 0.13idarctgX = -— i — djc. 7. rf [a / (jc)] = ad / (jc). 14.tf arcsin x = dx.
Смотрите также:
| Связь между графиком функции и графиком ее производной | Применение к приближенным вычислениям |
| Бесконечно малые величины | Применение дифференциала к различным задачам |

