Оглавление:



Диаграммы растяжения для пластичных и хрупких материалов
- Для пластмасс и хрупких материалов В предыдущем абзаце рассматривается физическое описание явления растяжения образца из пластического материала, такого как низкоуглеродистая сталь. Для других типов материалов, дающих пластическую деформацию при растяжении, получается примерно такая же диаграмма напряжений,
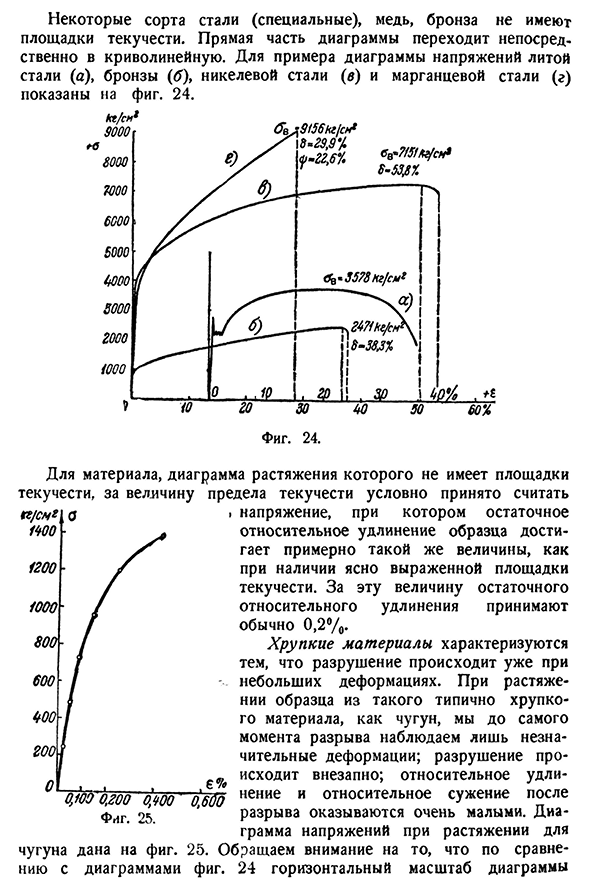
как показано на рисунке. 21.56 экспериментальное исследование[гл.] Некоторые марки стали (специальные), меди, бронзы не имеют предела текучести.
Прямая часть диаграммы переходит непосредственно в криволинейную часть. Например, диаграмма Людмила Фирмаль
напряжений литой стали (a), бронзы (tf), никелевой стали (b) и марганцевой стали (d) показана на рисунке. 24. Если диаграмма растяжения представляет собой материал, который не имеет предела текучести, предел текучести считается обычным К / см * около 140ОБУТ > Тысяча. Шесть сотен.- Шесть сотен. Четыреста. Две сотни. Одна тысяча двести Отчет 0>У0 0,200 0,400 ″ 0,600 Фигура. Двадцать
пять Напряжение, когда остаточное удлинение образца достигает приблизительно той же величины, что и при наличии четко определенной точки текучести. Для этого значение остаточного удлинения обычно составляет 0,2%. Хрупкий материал характеризуется тем, что разрушение происходит уже при небольших деформациях. При растяжении образца обычно хрупкого материала,
- такого как чугун, мы наблюдаем лишь незначительную деформацию вплоть до момента разрыва. Диаграммы растягивающих напряжений чугуна приведены на рисунке. 25. обратите внимание на то, что по сравнению с рисунком фигуры. 24 горизонтальная шкала сжатия диаграммы рисунок 57 Как правило, хрупкие материалы не сопротивляются росту-их прочность на растяжение невелика-примерно в 40 раз, и увеличивается вертикально Фигура. От 25 до 6 раз. По сравнению с прочностью на растяжение
пластмассы. Зависимость деформации от растягивающего напряжения хрупкого материала обычно недостаточна по закону крюка, и на рисунке вместо прямой части при малых напряжениях образуется слегка изогнутая линия. Таким образом, модуль упругости, равный касательной (§ 12) угла наклона относительно оси поперечной оси в контакте с диаграммой напряжений, фактически не может рассматриваться как постоянная величина такого материала. Из-за этих напряжений непосредственный модуль упругости из-за криволинейной выпуклости будет отличаться. Но
в пределах этих напряжений Между силой упругости е, Или Людмила Фирмаль
напряжение тока и co- Материал обычно функционирует в структурах, но отклонения от наблюдаемого закона крюка незначительны. Итак, в реальном расчете мы заменяем криволинейную часть рисунка соответствующим кодом(рис. 26) и постоянное рассмотрение модуля Е. Это связано с тем, что механические свойства хрупкого материала позволяют варьировать по отдельным образцам в более широком диапазоне, чем свойства пластического материала, можно определить взаимосвязь между напряжением и деформацией.
Смотрите также:

