Пример задачи 9.8
Деревянная консольная балка длиной l = 2 м прямоугольного поперечного сечения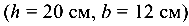 
нагружена сосредоточенной силой F = 5 кН в точке К под углом 
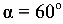к оси Z (рис. 9.12, а).
Проверить прочность и устойчивость балки, если R = 12 МПа, E = 10 ГПа.
Решение
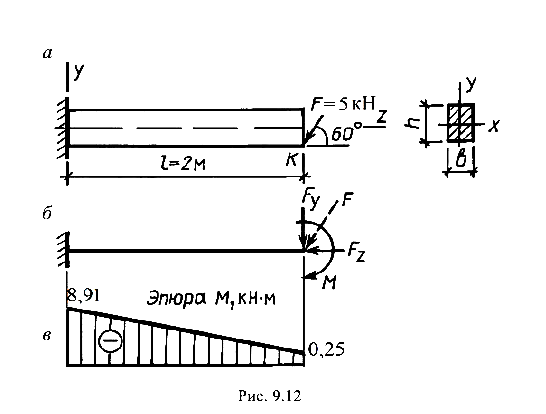
Составим расчетную схему балки.
Разложив действующую силу F на составляющие по направлению координатных осей, получим
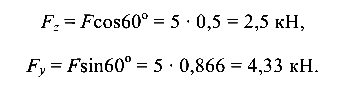
Перенесем составляющие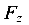 
и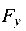 
к центру тяжести поперечного сечения балки, т. е. к оси Z. В результате образуются продольно сжимающая сила 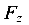= 2,5 кН, поперечно изгибающая сила 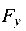= 4,33 кН и поперечно изгибающий момент
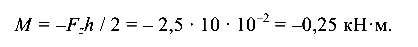
Расчетная схема балки показана на рис. 9.12, б, а эпюра изгибающих моментов — на рис. 9.12, в. Опасное сечение — защемление. Максимальный изгибающий момент
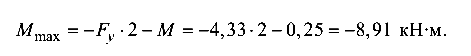
Анализ расчетной схемы показывает, что балка подвергается продольно-поперечному изгибу.
Вычислим геометрические характеристики балки: площадь сечения
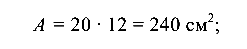
главные моменты инерции сечения
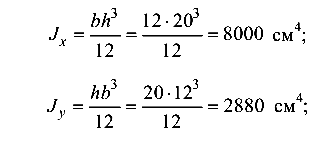
момент сопротивления сечения
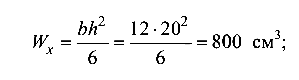
радиусы инерции сечения
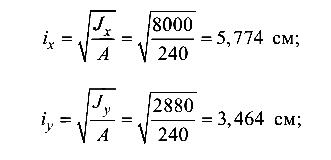
гибкости балки
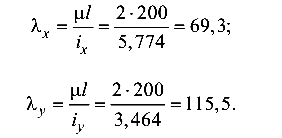
Проверка устойчивости ведется в плоскости наибольшей гибкости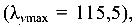 
т. е. относительно оси Y от продольно сжимающей силы .
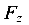При гибкости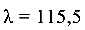 
коэффициент 
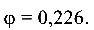Наибольшая допустимая продольная сила из (9.8)
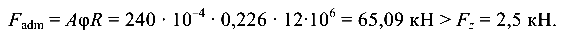
Устойчивость балки обеспечена.
Приступим к расчету на поперечный изгиб с учетом прогибов балки.
Прогиб балки в вертикальной плоскости, т. е. относительно оси Х, от силы 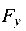и момента М (формулы взяты из справочника):
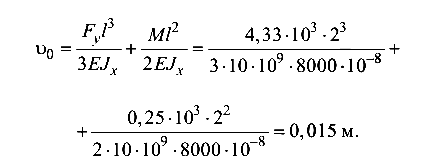
Эйлерова сила относительно оси X
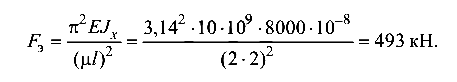
Полный прогиб балки от продольной и поперечной нагрузки
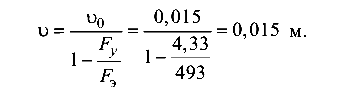
Полный изгибающий момент
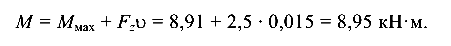
Максимальное нормальное напряжение в балке
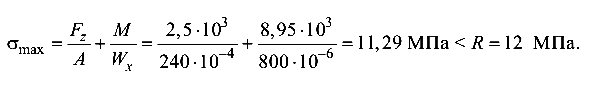
Этот пример решения задачи взят со страницы решения задач с примерами по всем темам предмета «Сопротивление материалов»:
Примеры решения задач по сопротивлению материалов
Дополнительные задачи которые вам будут полезны:
