Оглавление:














Дельта-метод
- Одним из эффективных методов качественного исследования нелинейных систем с 1 степенью свободы является Дельта-метод, предложенный Якобсеном в 1952 году. Можно создать приближенный портрет фаз системы без интегрирования дифференциальных уравнений. Дифференциальные уравнения часто связаны с утомительными вычислениями. Общее дифференциальное уравнение, описывающее движение неавтономных нелинейных систем при построении фазовых траекторий, т. е. Х к х-F х, а, 0.
Где x, A, H-координаты системы, ее 1-я и 2-я производные, A-круговая частота, t-время, f-функция нелинейного аргумента. L. S. Якобсен, общее решение-порядковое Обыкновенное дифференциальное уравнение по смещению второй фазы плоскости. Пмтф. Механика, т. 19, и 4, 1952, 543-553. Преобразуем исходное уравнение 6 в Дельта-форму. для этого введем безразмерное время x kt и соответствующую скорость v dxldx. И затем…
При этом теорема об изменении главного момента количеств движения системы материальных точек в относительном движении по отношению к центру инерции имеет вид, тождественный аналогичной теореме в абсолютном движении. Людмила Фирмаль
Можно написать формулу 6 Значение Дельта-функция, название от которой Они позвонили мне. Метод. Используйте обозначение 7, чтобы получить дифференциальное уравнение фазового локуса или Дельта-форму уравнения 6 из предыдущего уравнения. 8 b является функцией 3 аргументов, но в случае малых приращений Ax, Av, Am ее можно считать постоянной. Тогда уравнение 8 сразу интегрируется путем разделения переменных, в результате чего фазово-траекторные уравнения получаются в конечном виде х 6 в С2 г Где C — любая константа интегрирования, определенная из начального условия.
На фазовой плоскости Oxv уравнение 9 описывает семейство окружностей вокруг точки Qo −6 0.Поэтому небольшой отрезок фазовой траектории можно практически заменить дугой вокруг указанной точки. Вообще говоря, при переходе от одной дуги к другой абсцисса ее центра и радиуса изменяется. Однако в этом случае непрерывность фазового локуса не нарушается. То есть начало последующей дуги совпадает с концом предыдущей. Построение начинается в координатной точке x0×0 рис. 20.10, где vo v 0 определяется следующими начальными условиями тогда 0.Согласно тем же данным, Вы найдете величину 6a v0. т. И радиус Po Y x0 60 vJ. Однако вычислять радиус по формуле не имеет смысла.
Если центром точки Po и окружности Qo является Рой, то радиус измеряется как длина отрезка Q0P0 с помощью пары компасов. Из точки Qo, из центра радиуса Po Q0Pt, против часовой стрелки рисуется небольшая дуга окружности PaPi, что соответствует увеличению безразмерного времени t. Где D60-Радиан измерения первых дуг 10. 20. Используйте PBPlt и формулу 7 Для определения 6J 6×1 vt m .Тогда из центра радиуса p1 Q1pl Qi — br 0 вычерчивается следующая дуга Выражение J требует объяснения. Тогда приращение безразмерного времени Dm равно Радианной мере соответствующей дуги DO. Покажи мне. Отношение v — от dxldz 11 Между тем, из соображений фиг.
Если малые конечные приращения величин могут быть заменены этими различиями Vd 2 dv при 1 dx dl , 8. п 8jy дуплексный 12 Последний переход уравнения 12 основан на том, что он следует из Формулы 8. Если сравнить формулы 11 и 12, то получим 4m u, а следовательно, Dm D0. Поэтому на любом этапе построения фазовых траекторий соотношение ТДж м Дм м Д9. 13 Во многих случаях Дельта-функция зависит только от 1 аргумента x или v. Если она зависит только от t, то формула 6 линейна.
Таким образом, свободная вибрация консервативной системы является уравнением Х — — к х F х 14 с другой стороны, диссипация или автоколебание системы в зависимости от типа функции f описывается следующим уравнением А х F Т 15 А 8 зависит только от В. В этих случаях удобно создавать графики с функциями 6 6 x и 6 6 y .Эти Дельта-кривые характеризуют тип системы и степень ее nonlinearity. In в частности, для линейной системы 6 она будет равна нулю. Кроме того, если у вас есть Дельта-кривая, вы можете получить 8 требуемых значений непосредственно из чертежа, чтобы избежать соответствующих вычислений при построении фазовой трассы системы.
Задача 20.19. Создает фазовую траекторию для нелинейной колебательной системы, где сопротивление пропорционально 2-кратной скорости. Форма уравнения движения системы имеет вид Л л. Л Аах 0. 1 Начальные условия равны х 0 5.00, О А 0 0. 2 Коэффициент u 3 2×0.Исследуйте влияние количества шагов или длины дуги на точность построения. Решение. Если сравнить уравнения 1 и 6, то в этом случае f x,,, 0 — л Л Следовательно, 7 b CHEST м а Это означает, что сопротивление пропорционально 8.Дельта-кривая, определенная уравнением 3, показана на рисунке 5.Но сплошная линия. Обратите внимание, что на этом и следующем рисунке отклонение x нанесено вдоль оси ординат и пропорционально скорости.
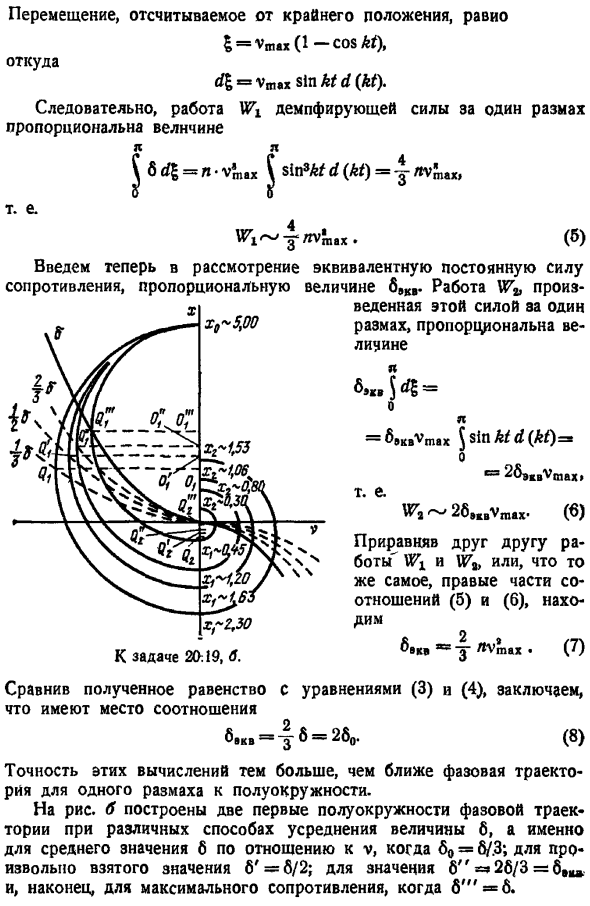
Ранг v-вдоль горизонтальной оси соответственно, точка изображения движется против часовой стрелки. Возвращаясь к построению фазовой траектории, следует отметить, что максимально возможная длина дуги равна полуокружности, а это соответствует 1 Качели колебаний. Поскольку длина дуги очень велика, кажется разумным предположить, что значение 6-это не значение в начальной точке, а некоторые средние значения, которые учитывают изменения 6 в этой дуге. Среднее значение значения 6 при изменении аргумента с нуля на текущее значение v равно 60 С. л в гор л в-Ле. 4 штрихованные кривые Диаграмма 60 показана на рисунке. И пунктирные линии.
В формуле 4 означает, что площадь треугольников на этом рисунке равна. Теперь вы можете легко построить фазовую траекторию, используя дугу максимальной длины, т. е. semicircle. To сделайте это, используйте компас и найдите центр первой дуги после серии попыток, чтобы сегмент был Нарисуйте дугу XoQi i, равную. Затем мы выбираем Центр Os 2-й дуги так, чтобы равенство Osx1 OjQj выполнялось, и строим 2-ю дугу фазовой траектории xg 2xg.
Продолжая этот процесс дальше, можно построить всю фазовую траекторию, которая представляет собой спиральную кривую, закрученную к началу координат для точек xD начало координат является специальной точкой, например стабильной focus. It соответствует стабильному равновесному состоянию x v 0, и система стремится вернуться после того, как она оценена из него. рассмотрим другие возможности усреднения значений в с. работу сопротивления в 1 качели можно найти в предположении, что фазовый локус представляет собой полукруг радиуса vmat.
Уже упоминалось, что сила сопротивления пропорциональна 6,а при допущениях она равна 6 6 lu2 pushah sin a Движение, которое вы считаете из крайнего положения 5 Vtnax 1-COS kt. Откуда виртуальная память. з грех КТ д КТ. Таким образом, поведение демпфирующая сила беспроводной доступ в 1 Качели 6d5 Н-В Н siifltfd Г. е. b с учетом величины постоянной силы, эквивалентной b ,.Работа выполняемая этой силой АА составляет 1 качание Затем мы вводим резистор, пропорциональный сопротивлению Ф ХВ-5.00 xg-1 3 VxvW. ГВБ з −2.30 pih — 6 взаимное уравнивание WJ и W или, то же самое, правая сторона корреляции 5 и 6 6, и Дж грех КТ Д т 26 ВМ Уравнения 3 и 4 Вопрос 20.19, б.
Равенство результатов и сравнение с отношениями 8 точность этих расчетов выше, поскольку фазовые траектории 1-го пролета ближе к полукругу. Рис. б, первые 2 полукруга фазовых траекторий построены различными способами для усреднения 6.То есть для среднего значения 6 относительно v, Если 60 6 3.Для любого значения 6 6 2 значение b 26 3 6 и, наконец, максимальное значение сопротивления, когда 6 равно 6 6 Возникает вопрос, какая из этих кривых является более точной. Ответ, Вообще говоря, получается путем построения фазовых траекторий с использованием большего количества шагов.
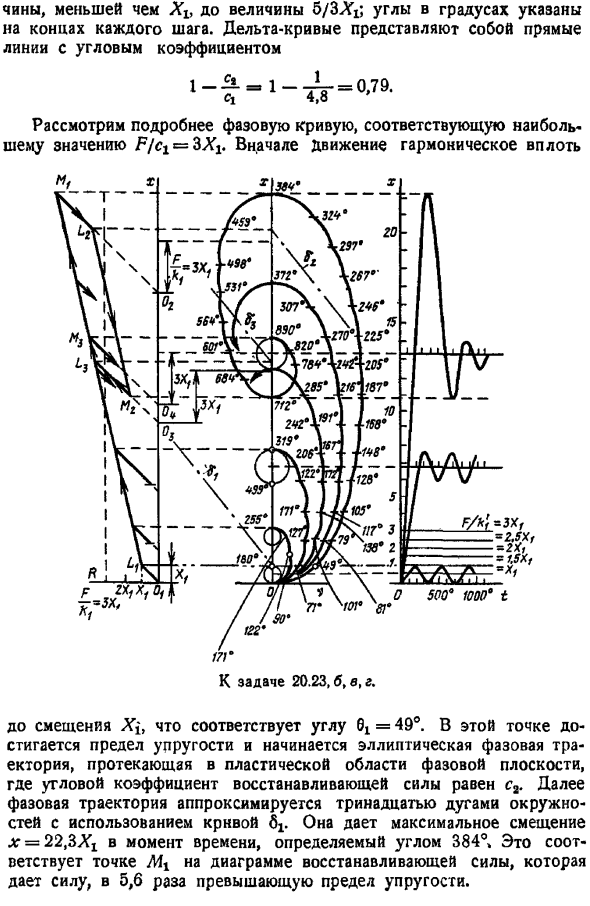
Однако в данном конкретном случае мы знаем точное численное решение задачи и получаем 1 54 и xt 0.94.Таким образом, максимальная точность выбранного минимального числа шагов является средним Дельта Кривая b кривые между 6 2 и 6 26 3, близкие к первой кривой. К задаче 20.49, c, d В общем случае решение с минимальным числом шагов, или 1 шаг на промежуток, даст удовлетворительные результаты только в том случае, если оно найдет достаточно надежный способ усреднения значения 6.Это противоречит известному факту, что при наличии сопротивления, пропорционального мощности 2 скорости, период колебаний уменьшается одновременно с уменьшением амплитуды, асимптотически приближаясь к значению 2 л л.
- На рисунке также показаны фазовые траектории, построенные с использованием 4 неравных шагов вдоль оси v в первом промежутке и с использованием 3 шагов во втором промежутке. Амплитуда Хг и XT несколько больше соответствующих значений, полученных в точном расчете, а длительность первого колебания и первого колебания измеряются под углом 206 и 388, respectively. As в результате наличие вторичного резистора увеличивает длительность первой развертки от i L. 206я 180А, то есть на 14, увеличение длительности первой вибрации первых 2 качаний равно -. Это 8 процентов. Наконец, построение фазового локуса фигуры d дается 9 шагами в первом диапазоне, 2 шагами в 4-м диапазоне.
Величина амплитуды Xj 1.55 при B 206 очень хорошо совпадает с точными значениями, показанными в скобках, и значение xa 0.95 также хорошо совпадает с точным значением 0.942. Подводя итог, мы приходим к выводу, что увеличение числа шагов всегда может повысить точность построения фазового локуса. Однако точность этой конкретной структуры может быть оценена только экспериментально путем увеличения числа шагов, если неопрятное решение является unknown. In кроме того, очевидно, что влияние длины дуги на точность конфигурации не везде одинаково на фазовой плоскости.
Разложим движение материальных точек системы на переносное поступательное вместе с осями декартовых координат, начало которых совмещено с центром инерции системы, и относительное движение по отношению к центру инерции. Людмила Фирмаль
При построении с несколькими шагами на пролет этот эффект будет более выраженным, а кручение траектории в сопряженной точке дуги будет больше. С инжиром. Этот изгиб определяется углом pt, p2 и т. д., и имеет примерно одинаковый порядок для всех сопряженных точек за исключением точки 4. г в пунктах 4, 5, 6 и 11 важнее. Задание 20.20.Движение физического маятника зависит от уравнения A2sin e 0. 1 f 0 создает фазовую траекторию маятника для следующих начальных условий а x0 36 0,2 л, vo 0 vo 0 vo 0 2 б х0 90 0.5 с ХV 180 я д начальная скорость достаточно велика, чтобы обеспечить непрерывное вращение маятника. Решение.
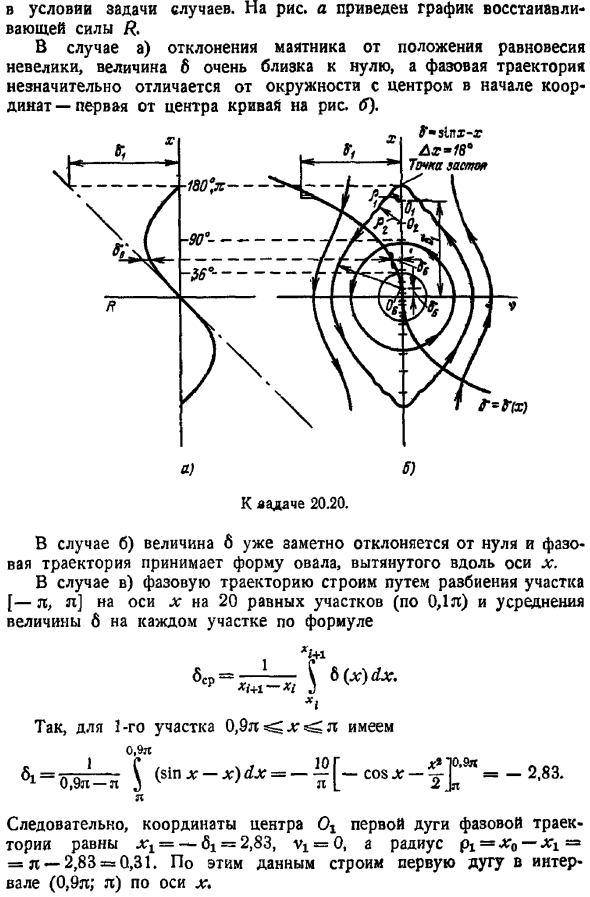
Преобразуем уравнение, приведенное в условиях задачи, в форму 1. Йе А х А х-sinx. 3 В этом деле f x, D 0 L x-с 2 6 6 x sin x-x. 4 Дельта-кривая, созданная этой формулой, показана на рисунке. b. все заданные фазовые траектории С точки зрения задачи дела. Рисунок R график восстанавливающей силы в случае а отклонение маятника от положения равновесия невелико, величина 6 очень близка к нулю, а фазовый локус несколько отличается от окружности вокруг начала координат первая кривая от центра фигуры. 5. Вопрос в 20.20. В случае b величина 6 уже значительно отклонилась от нуля, и фазовые траектории принимают форму вытянутых эллипсов вдоль оси X.
В случае c мы разделяем участок оси x — l, l на 20 равных участков каждый 0.1 l и строим фазовую орбиту, усредняя значение b для каждого участка по формуле. 6av — б х DX. Итак, на первом участке 0,9 л 61 d, 9 sinx-x b — Со Х У Й, 9-й-2.83. Я В результате координаты центра Og первой дуги фазовой траектории составляют xt — 6i 2.83, vx 0, а радиус pi x0-Xi л-2.83 0.31.На основе этих данных мы создадим первую дугу интервала 0.9 l l вдоль оси X. Аналогично, 2-й раздел 0.8 L x 0.9 l сказал он. -О. С. Н.-О.
Таким образом, координаты центра O2 2-й дуги фазовой траектории равны xt −6, 2.22 и vs 0.Радиус 2-й дуги p легче всего найти, измерив расстояние от точки Oa до конца первой дуги. После этого нарисуйте 2-ю точку интервала 0.8 l 0.9 th вдоль оси X. Далее таким же образом строим всю фазовую траекторию, учитывая, что она симметрична относительно обеих координатных осей. Орбита даже сильнее, чем случай b и простирается вдоль оси X. Обратите внимание, что траектория намеренно имеет неправильную форму вблизи точки x л.
Это очевидно, потому что величина o стремится к x, потому что x стремится к 1, и в результате радиус фазового локуса стремится к нулю, потому что v 0 в этих точках. Однако неточность этой структуры мало влияет на точки, достаточно удаленные от указанных, например, на пересечении орбиты с орбитой v-axis. It определяет максимальную скорость вибрации vmax, равную в этом случае 2. Фазовый Локус в локусе случай c представляет собой замкнутую кривую, окружающую начало координат.
Для всех таких траекторий начало координат является особой точкой типа Центра. Наконец, в случае d фазовая траектория представляет собой открытую бесконечную кривую, простирающуюся вдоль оси X. Маятник не вибрирует, а вращается вокруг точки подвеса с положительной или отрицательной переменной угловой скоростью. Задача 20.21.Объект M с массой m расположен на горизонтальной плоскости. К корпусу прикреплена вертикальная пружина рисунок а а с Вопрос 20.21, а, б. Ом я, коэффициент жесткости равен С. в первоначальное вертикальное положение, пружина не растянута. Создайте дифференциальное уравнение для вибрации небольшого объекта вдоль горизонтальной линии x.
Создайте фазовый портрет динамической системы. Решение. Восстанавливающая сила пружины, пропорциональная удлинению пружины, направленному от Mx к O, действует на тело. Если обозначить координаты точки Mi через x, MMt x, то коэффициент силы F r-ctyr — i oh Маршрут в ряд Ограничившись первыми 2 членами серии 2 Так, при незначительном отклонении тела от вертикального равновесия сила F пропорциональна 2 степени отклонения. Определить проекцию силы F на ось V. cosa — — fl — I 1 2 71 7 l f найдено Fx Fcosa jX3 Дифференциальные уравнения для малых колебаний ТХ — й — г ЭМ, — 2da 0 для краткости Л Х 0.
Так, восстанавливающая сила при незначительном отклонении объекта от положения равновесия в данном случае пропорциональна 3-й степени отклонения объекта. Приступайте к построению фазового портрета системы. Перепишите выражение 3 в следующем формате Я Х Х — Х 4 Где его найти Б А х — ДХ — .И затем Из Формулы b видно, что если x klV , то 6 равно нулю. Это означает, что в соответствующей точке центр дуги, которая приближается к фазовому локусу, находится в начале координат. На рис. 1 представлен график восстановительной силы-кубическая парабола, а на рис.
Дельта-кривые и фазовые траектории 3 энергетических уровней начальные координаты и скорость, принимающие p A 0,4.Фазовые траектории строятся с равными шагами Dx 0,2 вдоль оси X. ГТ — х-0,их — в На рисунке показаны первый и шестой шаги максимальных фазовых траекторий. При малых перемещениях и скоростях фазовые траектории имеют форму небольших эллипсов, которые сильно простираются вдоль оси x, вокруг оси origin. As уровень энергии увеличивается, траектория приближается к прямоугольнику. Короткая сторона прямоугольника параллельна оси X, а центр совпадает с началом. Начало координат-сингулярность, подобная центру, но точка фазы не движется по кругу.
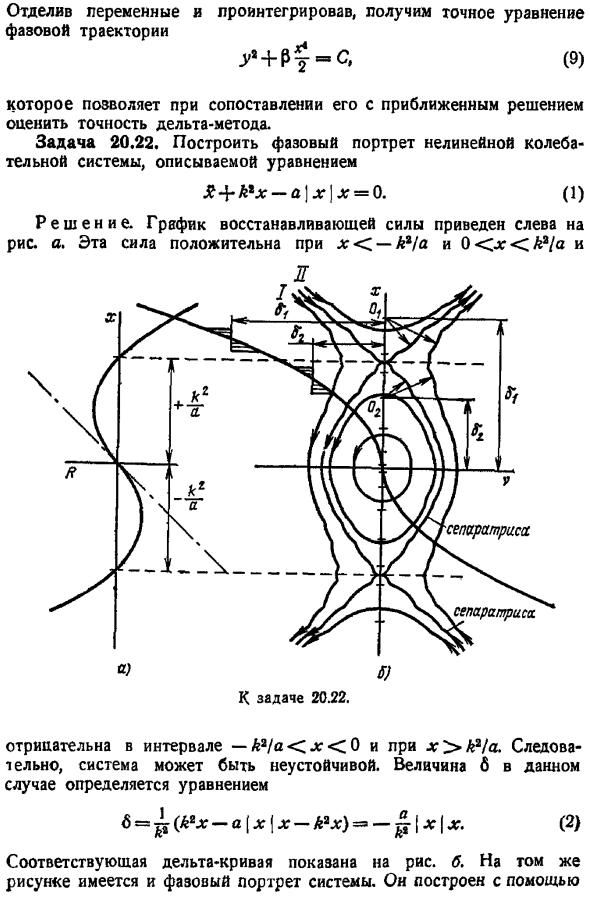
Обратите внимание, что проблема может быть решена exactly. In факт, уравнение 3 можно записать в виде системы С-СР с Разделить 6 на 7 Если разделить и интегрировать переменные, то получится точное уравнение траектории движения фага ГХЦГ-РУ-с, 9 При сравнении с приближенным решением можно оценить точность Дельта-метода. Задача 20.22.Создание фазового портрета нелинейной колебательной системы, описываемой уравнением к Х- Х Х. 1 Решение G представляет собой график восстанавливающей силы, показанный слева от рисунка. a. эта сила приложена к x — P1a и 0 x La a и Выпуск 20.22. Если интервал отрицательный-A a x 0 и x fc2 A. следовательно, система может стать нестабильной.
Значение 6 в данном случае определяется выражением — А Х Х-Х — — Х Х. 2 Соответствующая Дельта-кривая показана на рисунке. b. In тот же рисунок, Есть также портрет фаз system. It построен с использованием Маленький и неравный шаг Dx. Это сделает повреждение приблизительного локуса фазы более четко видимым. Характерными точками на фазовой плоскости являются точки x Aa a, va 0.Их можно назвать застойными точками.
Это связано с тем, что точка фазы в них неподвижна, поэтому графическое определение времени невозможно. Однако даже достаточно грубая геометрическая конфигурация дает очень точную информацию о внутренних характеристиках системы. Фазовые траектории, проходящие через точку застоя выше, называются сепаратрисами.
Смотрите также:
Предмет теоретическая механика

