Оглавление:
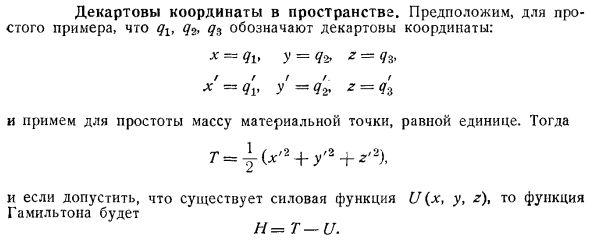



Декартовы координаты в пространстве
- Как простой пример, glt q предположим, q представляет декартовы координаты. = ду у = 3к Х = = Г З З = М 3. Он также принимает массу важной точки равной одной точке для простоты. И затем… Р = г х 2 + 2 + р 2 И если предположить, что силовая функция U x, y, z существует, то Гамильтонова функция имеет вид Г И. Эта функция должна быть выражена во вспомогательных переменных pj, p2 Pz , определяемых переменными x, y, z и выражением. Функция Гамильтона Ч = Р1 + пр + Р3 и Х Я. В результате канонические уравнения ДХ ды ДЗ ДТ ДТ ПБ П ДТ П ДП ю АКДС ДПС дю дю dt dx t dy 1 dt dz. Если вы исключите переменную p из этих уравнений, это, очевидно, будет нормальное уравнение движения.
Оно показывает, что движение не изменится, если деформировать кривую, не изменяя ее длины, и изменять при этом силу таким образом, чтобы не изменялась ее касательная составляющая. Людмила Фирмаль
Давайте посмотрим на результаты метода Якоби в этом случае. Этот метод то, что вам нужно найти для дифференциальных уравнений dt Полный Интеграл, то есть Интеграл, содержащий 3 Неаддитивные константы.
- Потому что время явно не входит в это уравнение В = ГТ + ж х, у, Z. Где h константа, и достаточно, чтобы функция W удовлетворяла следующему соотношению: Для этого уравнения с 3 переменными, вы найдете полный Интеграл Если х, Г, Г, А, , Л Если он содержит 2 новые константы a и p, и ни одна из них не является аддитивной, то теорема Якоби указывает, что конечные уравнения движения являются дв да Первые 2 уравнения представляют траекторию движения, а последнее определяет, сколько времени точка движения потратит на достижение определенного положения в ней orbit.
Кроме того, для pb pb pb p3 получается значение dV dV dV P1 dx DY RL dz И p1r p2, p здесь x , y , z и V равны ht W x, y, z , поэтому эти формулы определяют проекцию скорости точки. Одна функция IF. Эта функция удовлетворяет выражению J 4 Р4 г р + р 2 = г + л Это просто интеграл кинетики energy. So как мы уже видели, а постоянная интеграла кинетической энергии. Кстати, вы можете легко проверить геометрические характеристики локуса. Приведем некоторые определенные значения констант a, A.
Тогда скорость никогда не обратится в нуль и движущаяся точка будет бесконечное число раз оборачиваться по своей траектории. Людмила Фирмаль
Приведенные выше уравнения для x , y и r из за частных производных функции IF показывают, что в каждой точке x, y, r скорость перпендикулярна скорости поверхности IF const. Проблемы локуса Эта траектория приобретается, если эта траектория выбрана для прохождения через местоположение движущейся точки в question. As в результате все орбиты, полученные путем изменения a , перпендикулярны поверхности, если = const.
Смотрите также:
Решение задач по теоретической механике

