Оглавление:
Действия с корнями (радикалами)
а) Арифметический корень n-й степени из числа а (обозначается 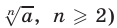 — неотрицательное число, n-я степень которого равна а , т.е. если
— неотрицательное число, n-я степень которого равна а , т.е. если 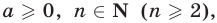 то
то
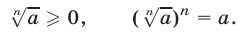
Если n = 2, то арифметический корень из числа а обозначается 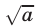 и называется арифметическим квадратным корнем.
и называется арифметическим квадратным корнем.
б) Свойства арифметического корня 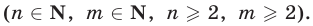
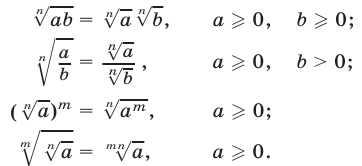
в) Для любого 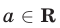 справедливо равенство
справедливо равенство
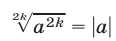
и, в частности,
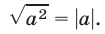
г) Если 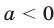 , то
, то
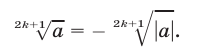
д) Формула «сложного радикала». Если 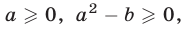 то
то
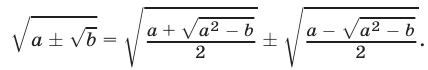
Пример №17.
Упростить выражение
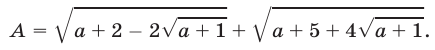
Решение:
Выражение имеет смысл при  Заметив, что
Заметив, что 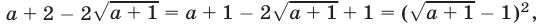
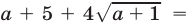
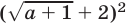 , и применив формулу
, и применив формулу 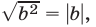 получим
получим
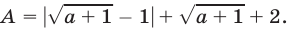
Если 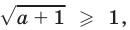 то
то 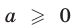 и тогда
и тогда 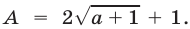 Если
Если 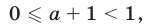 т. е.
т. е. 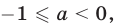 то
то 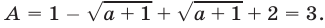
Ответ:

Пример №18.
Упростить выражение
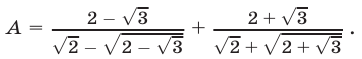
Решение:
Умножив числители и знаменатели дробей на 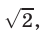 запишем А в следующем виде:
запишем А в следующем виде:
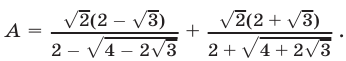
Так как 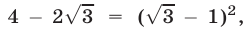
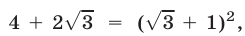 то имеем
то имеем 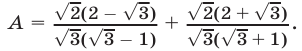
Приводя дроби к общему знаменателю, получаем
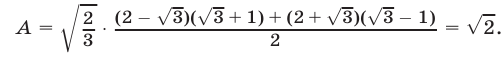
Замечание. Тот же результат можно получить, применив формулу «сложного» радикала, в силу которой имеет место
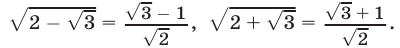
Этот материал взят со страницы решения задач с примерами по всем темам предмета математика:
Возможно вам будут полезны эти страницы:
| Разложение многочлена на множители примеры с решением |
| Производные пропорции примеры с решением |
| Степень с рациональным и действительным показателем примеры с решением |
| Логарифмы примеры с решением |

