Действия над векторами, заданными проекциями

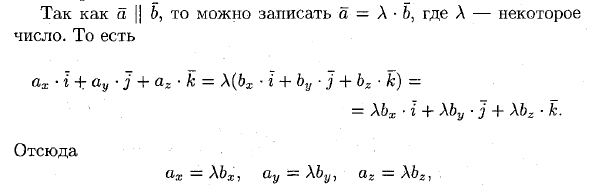
Действия над векторами, заданными проекциями

• Действие, предпринятое по вектору проекция Задайте векторы a- (ax \ ay \ az) и b = (bx; by] bz) с проекциями на оси Ox, Oy, Oz или аналогичные a = ax-i + ay • j. + az • k, b = bx i + by • j + bz • k. Линейные векторные операции Поскольку векторные линейные операции сводятся к соответствующим линейным операциям проекций этих векторов, мы можем написать: 1.а ± b = (ax ± bx) i 4- (av ± by) j 4- (az ± bz) ky или просто a ± b = (ax ± bx \ ay ± by \ az ± bz).

То есть, когда вектор умножается на скаляр, координаты вектора умножаются на этот скаляр. Вектор уравнения Из определения вектора как ориентированного отрезка, который может двигаться в пространстве параллельно самому себе, два вектора a и b равны, только если выполняется уравнение: ax = bX} ay = by) az = т.е. (Ox = bx) ay-by, a2 = bz. Векторная коллинеарность Найти условие коллинеарности для векторов a и 6, заданных координатами.

То есть, когда вектор добавляется (вычитается), добавляется та же самая координата имени (вычитается). 2. \ a = \ ax-r 4- Aau • j + \ az • k или короче, чем Ha ​​= (Aag; Aau; Aa2). Людмила Фирмаль

С тех пор вы можете написать | 6, a = A • 5. Где А — это конкретное число Это ах • g + ay • j + az • k = \ (bx-g + by • j + bz • k) = = Xbx • i + \ by ■ j -f- Xb2 • k. Отсюда ax = A6X, ay = аг = Л62, Следовательно, проекция коллинеарного вектора пропорциональна. Обратное также верно. Векторы с пропорциональными координатами находятся на одной линии.

Координаты точки Предположим, что декартова декартова система координат Oxyz задана в пространстве. Для любой точки M координаты вектора OM называются координатами точки M. Вектор OM называется радиус-вектором точки M и обозначается r.

• Решение задач по высшей математике

Проекция вектора на ось	Скалярное произведение векторов и его свойства
Разложение вектора по ортам координатных осей. Модуль вектора направляющие косинусы	Выражение скалярного произведения через координаты. Применение скалярного произведения векторов

Примеры решения и задачи с методическими указаниями

Решение задач	Лекции
Сборник и задачник	Учебник

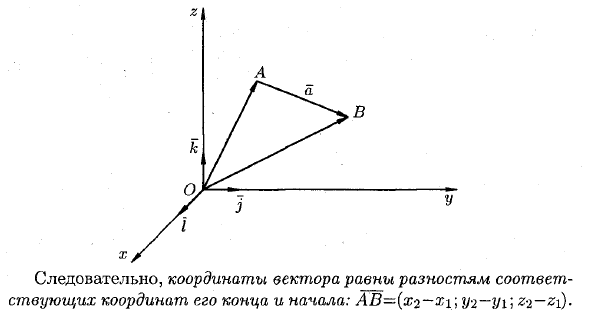
• То есть OM = r. Следовательно, координаты точки являются координатами ее радиус-вектора. f = (i; y; z) или r = x * i + y- j + z * k Координаты точки M записываются в формате M (x \ y \ z). Векторные координаты Если вам известны координаты точек A (xi; y \ ‘, z ) и B (x2 \ Y2 \% r), найдите координаты вектора a-AB-have (см. Рисунок) AB = OB-OA = (x2 • i + Y2 • 3 + • C- (xx • t + yi •] + z \ • k) — = (X-2-Xi) i + (y2-yi) j + (z2-Zi) k.

В результате координаты вектора равны разности между соответствующей конечной и начальной координатами: AB = (x2 — a? I; 2/2 — Y1 | 22— £ 1) •