Декартовой системой координат в пространстве называется совокупность точки и базиса.
Точка называется началом координат или полюсом. Прямые, проходящие через начало координат в направлении базисных векторов, — осями координат. Первая прямая — осью абсцисс, вторая — осью ординат, третья — осью аппликат. Плоскости, проходящие через оси координат, называются координатными плоскостями.
Вектором 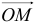 , начало которого совпадает с началом координат, а конец находится в точке
, начало которого совпадает с началом координат, а конец находится в точке 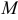 , называется радиус-вектором точки
, называется радиус-вектором точки 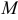 .
.
Базис называется ортонормироваиным, если его векторы попарно ортогональны (перпендикулярны) и по длине равны единице.
Декартова система координат, базис которой ортонормирован, называется декартовой прямоугольной системой координат
1. Если задана тройка попарно перпендикулярных единичных векторов, то каждый вектор пространства можно единственным способом разложить по векторам 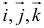 :
: 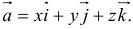 . Числа
. Числа 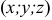 называют координатами вектора
называют координатами вектора 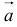 в базисе
в базисе 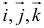 и обозначают
и обозначают 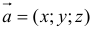 .
.
Теорема. Декартовы прямоугольные координаты 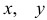 и
и 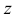 вектора
вектора 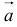 равны проекциям этого вектора на оси
равны проекциям этого вектора на оси 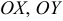 и
и 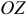 соответственно.
соответственно.
На рис.8 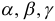 — углы наклона вектора
— углы наклона вектора 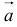 к осям
к осям 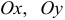 и
и 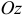 соответственно.
соответственно.
2. Длина вектора 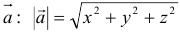
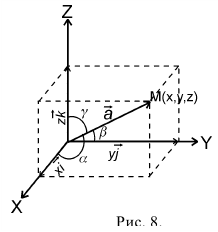
3. Направляющие косинусы вектора 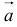 (Рис. 8).
(Рис. 8).
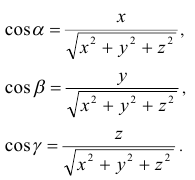
Возведем в квадрат три равенства и, складывая их, получим:
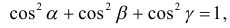
т.е. сумма квадратов направляющих косинусов любого вектора равна
единице.
4. Орт вектора 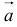 :
: 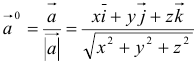
5. Пусть даны векторы 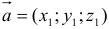 и
и 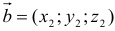
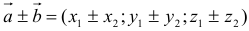 координаты алгебраической суммы векторов равны алгебраической сумме соответствующих координат слагаемых.
координаты алгебраической суммы векторов равны алгебраической сумме соответствующих координат слагаемых.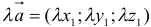 , где
, где 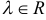 координаты произведения вектора на число равны произведению соответствующей координаты на это число.
координаты произведения вектора на число равны произведению соответствующей координаты на это число.
6. Пусть даны точки 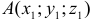 и
и 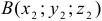 . Чтобы найти координаты (компоненты) вектора
. Чтобы найти координаты (компоненты) вектора 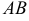 , нужно из координат точки его конца вычесть координаты его начала:
, нужно из координат точки его конца вычесть координаты его начала: 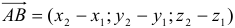 .
.
Расстояние между двумя точками: 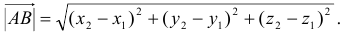
7. Если 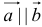 , то
, то 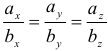 . (Если векторы коллинеарны, то их координаты пропорциональны).
. (Если векторы коллинеарны, то их координаты пропорциональны).
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Высшая математика краткий курс лекций для заочников
Возможно вам будут полезны эти страницы:
| Векторная алгебра: основные понятия и определения |
| Проекция вектора на ось |
| Скалярное произведение двух векторов |
| Полярная система координат |
