Оглавление:
Действия над матрицами
Сложение
Операция сложения матриц вводится только для матриц одинаковых размеров.
Суммой двух матриц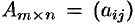 
и 
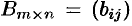называется матрица 
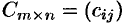такая, что 
(
, 
).
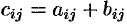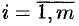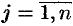Пример №1.2.
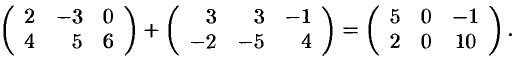
Аналогично определяется разность матриц.
Умножение на число
Произведением матрицы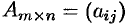 
на число 
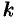называется матрица 
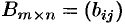такая, что 
.
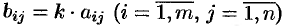Пример №1.3.
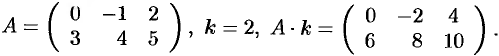
Матрица —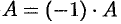 
называется противоположной матрице 
.
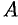Разность матриц 
можно определить так: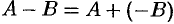 
. Операции сложения матриц и умножения матрицы на число обладают следующими свойствами:
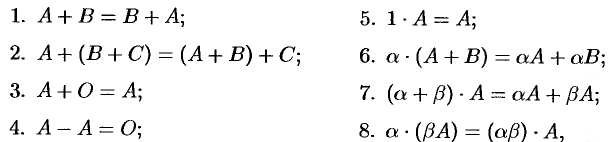
где ,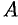 
, 
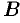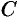— матрицы, 
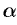и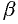 
— числа.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Свойства преобразования Лапласа |
| Обратное преобразование Лапласа |
| Элементарные преобразования матриц |
| Системы линейных однородных уравнений |
