Действия над комплексными числами в тригонометрической форме
Пусть заданы два комплексных числа в тригонометрической форме:
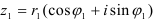
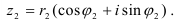
Умножение:
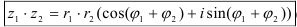
при умножении комплексных чисел в тригонометрической форме их модули перемножаются, а аргументы складываются.
Деление:
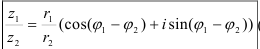
при делении комплексных чисел в тригонометрической форме их модули делятся, а аргументы вычитаются.
Возведение в степень:
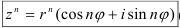
при возведении в степень комплексного числа в тригонометрической форме модуль числа нужно возвести в 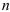 -ю степень, а аргумент умножить на
-ю степень, а аргумент умножить на 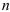 .
.
Извлечение корня 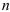 -й степени: корень
-й степени: корень 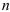 -й степени из числа
-й степени из числа 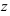 имеет ровно
имеет ровно 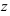 значений, которые находятся по формуле:
значений, которые находятся по формуле:
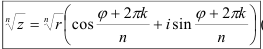
Для их нахождения необходимо менять значения параметра 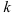 начиная с
начиная с 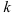 = 0 (первый корень
= 0 (первый корень 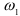 ), затем
), затем 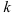 = 1 (второй корень
= 1 (второй корень 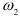 ) и т.д. до
) и т.д. до 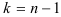 (
(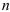 -й корень
-й корень 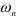 ).
).
Рассмотри, как выполняются операции над комплексными числами в тригонометрической форме на конкретных примерах.
Пример решения заказа контрольной работы №124.
Для комплексных чисел
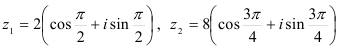
найдите:
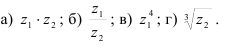
Решение:
а) Согласно формуле (1) получим
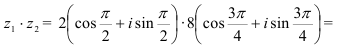
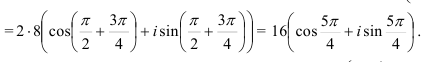
Используя формулу (2), находим
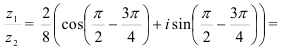
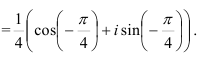
в) Применяя формулу (3), находим
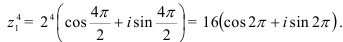
г) Для извлечения кубического корня из 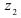 воспользуемся формулой (4):
воспользуемся формулой (4):

где параметр 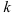 будет принимать значения 0, 1 и 2
будет принимать значения 0, 1 и 2
(поскольку число корней 3-й степени из числа имеет ровно 3 значения).
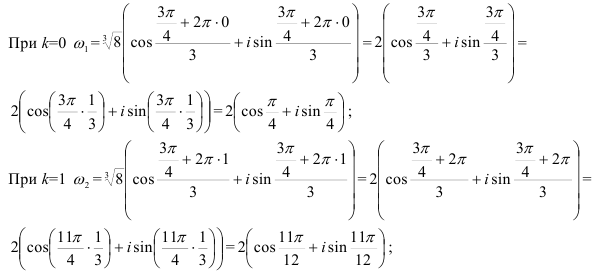
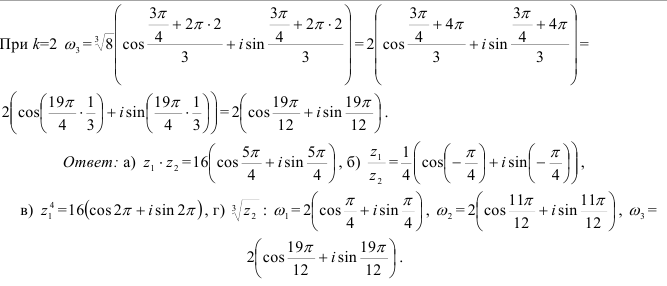
На этой странице вы сможете заказать контрольную работу и познакомиться с теорией и другими примерами решения:
Заказать контрольную работу по высшей математике
Другие похожие примеры возможно вам будут полезны:
| Контрольная работа: Приложении определённого интеграла |
| Переход от алгебраической формы к тригонометрической и показательной |
| Операция деления для комплексных чисел |
| Решение задачи Коши |

