Оглавление:
Сложение комплексных чисел
Суммой двух комплексных чисел 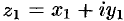 и
и 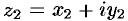 называется комплексное число, определяемое равенством
называется комплексное число, определяемое равенством
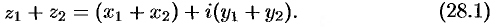
Сложение комплексных чисел обладает переместительным (коммутативным) и сочетательным (ассоциативным) свойствами:
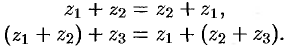
Из определения (28.1) следует, что геометрически комплексные числа складываются как векторы (см. рис. 163).
Непосредственно из рисунка видно, что 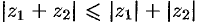 . Это соотношение называется неравенством треугольника.
. Это соотношение называется неравенством треугольника.
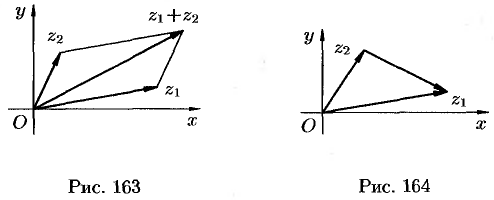
Вычитание комплексных чисел
Вычитание определяется как действие, обратное сложению. Разностью двух комплексных чисел 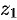 и
и 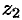 называется такое комплексное число
называется такое комплексное число 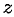 , которое, будучи сложенным с
, которое, будучи сложенным с 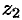 , дает число
, дает число 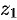 , т. е.
, т. е. 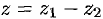 , если
, если 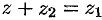 .
.
Если 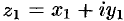 ,
, 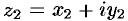 , то из этого определения легко
, то из этого определения легко
получить 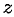 :
:
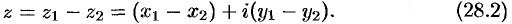
Из равенства (28.2) следует, что геометрически комплексные числа вычитаются как векторы (см. рис. 164).
Непосредственно из рисунка видно, что 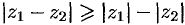 . Отметим, что
. Отметим, что
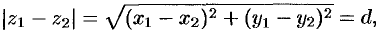
т. е. модуль разности, двух комплексных чисел равен расстоянию 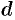 между точками, изображающими эти числа на плоскости.
между точками, изображающими эти числа на плоскости.
Поэтому, например, равенство 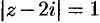 определяет на комплексной плоскости множество точек
определяет на комплексной плоскости множество точек 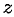 , находящихся на расстоянии 1 от точки
, находящихся на расстоянии 1 от точки 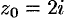 , т. е. окружность с центром в
, т. е. окружность с центром в 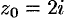 и радиусом 1.
и радиусом 1.
Умножение комплексных чисел
Произведением комплексных чисел 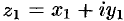 и
и 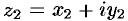 называется комплексное число, определяемое равенством
называется комплексное число, определяемое равенством
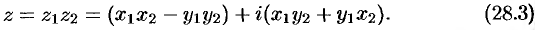
Отсюда, в частности, следует важнейшее соотношение

Действительно, 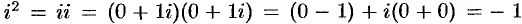 . Благодаря соотношению (28.4) формула (28.3) получается формально путем перемножения двучленов
. Благодаря соотношению (28.4) формула (28.3) получается формально путем перемножения двучленов 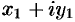 и
и 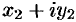 :
:
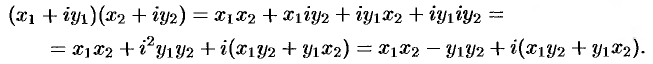
Например,
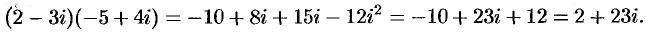
Заметим, что 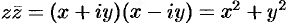 — действительное число.
— действительное число.
Умножение комплексных чисел обладает переместительным, сочетательным и распределительным (дистрибутивным) свойствами:
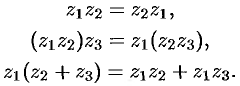
В этом легко убедиться, используя определение (28.3).
Найдем произведение комплексных чисел 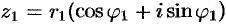 и
и 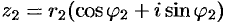 , заданных в тригонометрической форме:
, заданных в тригонометрической форме:
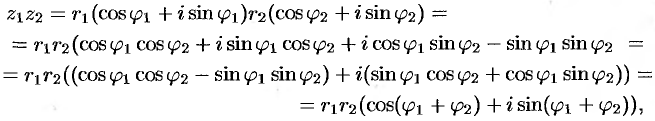
т.е.
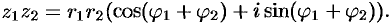
Мы показали, что при умножении комплексных чисел модули перемножаются, а аргументы складываются.
Это правило распространяется на любое конечное число множителей. В частности, если есть  множителей и все они одинаковые, то
множителей и все они одинаковые, то
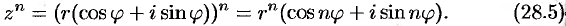
Формула (28.5) называется формулой Муавра.
Пример №28.1.
Найти 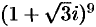 .
.
Решение:
Запишем сначала число 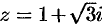 в тригонометрической форме:
в тригонометрической форме:
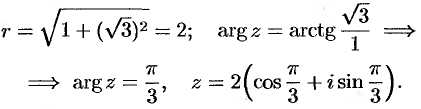
По формуле Муавра имеем
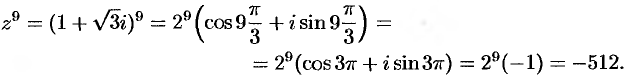
Деление комплексных чисел
Деление определяется как действие, обратное умножению. Частным двух комплексных чисел 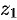 и
и 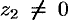 называется комплексное число
называется комплексное число 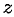 , которое, будучи умноженным на
, которое, будучи умноженным на 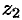 , дает число
, дает число 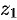 , т. е.
, т. е. 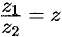 , если
, если 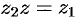 .
.
Если положить 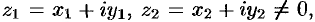
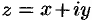 , то из равенства
, то из равенства 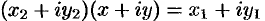 следует
следует
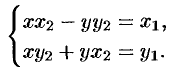
Решая систему, найдем значения  и
и  :
:
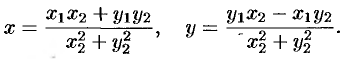
Таким образом,
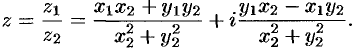
На практике частное двух комплексных чисел находят путем умножения числителя и знаменателя на число, сопряженное знаменателю («избавляются от мнимости в знаменателе»).
Пример №28.2.
Выполнить деление 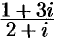 .
.
Решение:
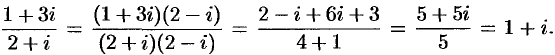
Для тригонометрической формы комплексного числа формула деления имеет вид
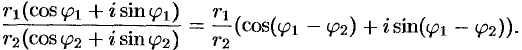
При делении комплексных чисел их модули, соответственно, делятся, а аргументы, соответственно, вычитаются.
Извлечение корней из комплексных чисел
Извлечение корня  -й степени определяется как действие, обратное возведению в натуральную степень.
-й степени определяется как действие, обратное возведению в натуральную степень.
Корнем  -й степени из комплексного числа
-й степени из комплексного числа 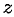 называется комплексное число
называется комплексное число 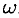 , удовлетворяющее равенству
, удовлетворяющее равенству 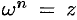 , т. е.
, т. е. 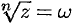 , если
, если 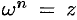 .
.
Если положить 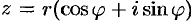 , а
, а 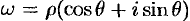 , то, по определению корня и формуле Муавра, получаем
, то, по определению корня и формуле Муавра, получаем
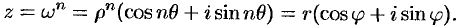
Отсюда имеем 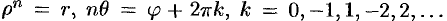 To есть
To есть 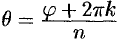 и
и 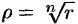 (арифметический корень).
(арифметический корень).
Поэтому равенство 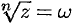 принимает вид
принимает вид
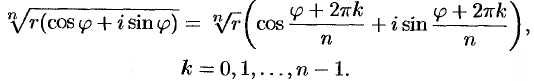
Получим  различных значений корня. При других значениях
различных значений корня. При других значениях 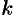 , в силу периодичности косинуса и синуса, получатся значения корня, совпадающие с уже найденными. Так, при
, в силу периодичности косинуса и синуса, получатся значения корня, совпадающие с уже найденными. Так, при 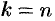 имеем
имеем
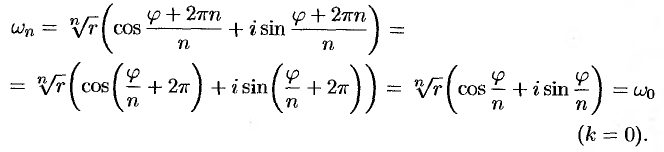
Итак, для любого 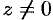 корень
корень  -й степени из числа
-й степени из числа 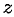 имеет ровно
имеет ровно  различных значений.
различных значений.
Пример №28.3.
Найти значения 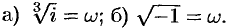
Решение:
а) Запишем подкоренное выражение в тригонометрической форме: 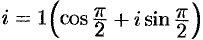 . Стало быть,
. Стало быть,
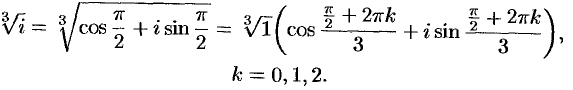
При 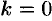 имеем
имеем
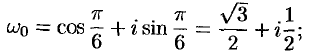
при 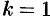 имеем
имеем
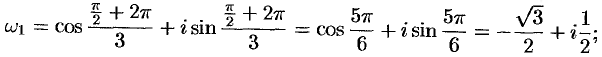
при 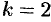 имеем
имеем
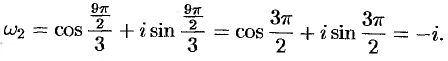
б) Снова запишем подкоренное выражение в тригонометрической форме:
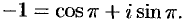
Поэтому
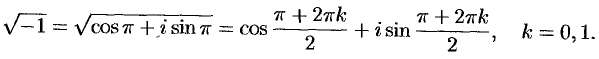
При 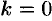 получаем
получаем 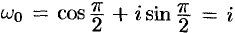 , а при
, а при 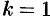 получаем
получаем 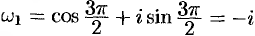 . Таким образом,
. Таким образом, 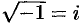 и
и 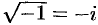 .
.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Геометрическое изображение комплексных чисел |
| Формы записи комплексных чисел |
| Свойства неопределенного интеграла |
| Метод непосредственного интегрирования |

