Оглавление:


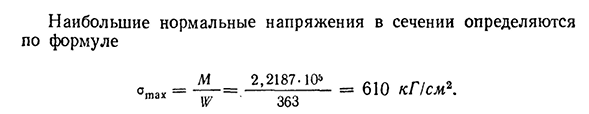

Действие на бесконечно длинную балку нескольких сосредоточенных сил и равномерно распределенной нагрузки
- Действие на бесконечно длинном луче Какая-то концентрированная сила И равномерно распределенная нагрузка Рассмотрим случай, когда два концентрата и RG действуют на пучок бесконечной длины(рис. 290, а). Из действия этих сил необходимо выяснить
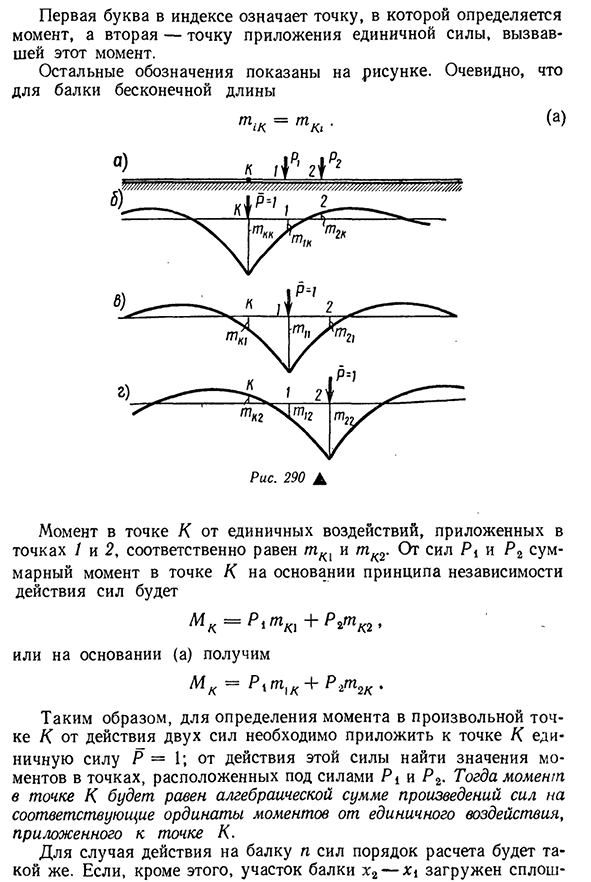
момент любого поперечного сечения K. _ примените отдельно один эффект P=1 в точках K, 1 и 2, и построим график M из этих эффектов(рис. 290, б, c и D). Вводится обозначение: — момент точки/C, вызванный действием единичной силы, приложенной в точке
K\t1k-единичная сила, приложенная в точке K Первая буква индекса 334 Людмила Фирмаль
указывает точку,в которой определяется момент, а вторая-точку приложения единичной силы, вызвавшей этот момент. Остальные символы показаны на рисунке. Понятно, что для пучка бесконечной длины (И) Точки K моменты от единичного удара, приложенного в точках 1 и 2, равны соответственно TK1 и TK2. На основе принципа действия силы в точках K и P2 сумма моментов маны не зависит от
действия силы воли Или, основываясь на (a)、 МК=Р^т1к+Р^Т2К • Поэтому для того, чтобы определить момент в любой точке К от действия двух сил, необходимо приложить к точке к единственную силу Р=1,а от действия этой силы Р1 далее, момент точки к равен сумме произведения силы на соответствующую вертикальную ось точки К. Для случая действия на балку n-силы процедура расчета
- будет такой же. Если, кроме того, балка X2 сечения-полностью нагружена- 335 равномерное распределение нагрузки по прочности составляет 7 фиг. 291, б), момент в точке к этой нагрузки обозначен М. Чтобы определить этот момент, разделите распределенную нагрузку на базовую силу DX\умножив моменты, соответствующие этим силам TPC в диапазоне от y до x2. =] * дых-ТП К~Д УКТ а=Ди> Си Рис. 291, конечное выражение момента при нагружении балки, приведенное в виде b=P+P-2t2k4 — +P+I= Аналогично, отклонение, угол поворота и боковая сила могут быть найдены в сечении бесконечно длинной
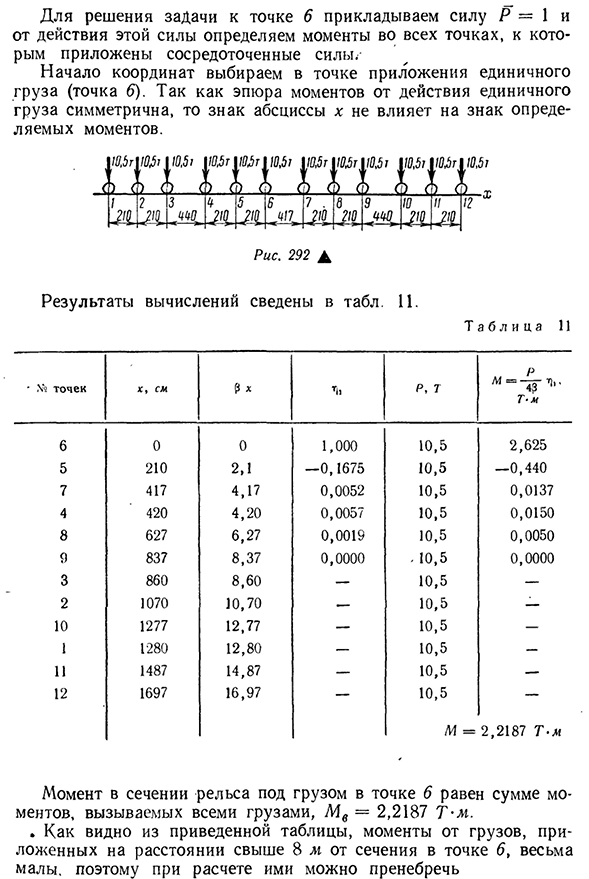
балки под действием нескольких концентратов и равномерно распределенных нагрузок. П р и М Е Р. изгибающий момент и напряжение от нагрузки на поперечном сечении железнодорожного рельса типа Р65 при нагрузке в точке 65, нагрузка на тепловоз ТЭЗ показана на рисунке 292. * Коэффициент к принимается равным 300кпсм2, жесткость рельса=2-106-3573 кг-см2, момент сопротивления? = = 363 см3. Триста. 4-2-106-3573 Один. Сто. Для решения задачи к 336 точкам 6 приложим силу Р-1, и от действия этой силы определим момент во всех точках, на которые приложена способность концентрироваться. Начало координат выбирается
в точке приложения единичной нагрузки (точка 6). Поскольку график Людмила Фирмаль
момента от действия единичной нагрузки симметричен, знак поперечной к не влияет на знак определяемого момента. P и s 2 9 2A Один. < 110,5 г’ ) <) ( 10,5 т ) ( 10,5 т ш т110. 5т1ю. 5Т\ \ Sht1yu. 5Т110. 5Tu Вт т110. Пять О) Л Два. Л , Три. СП Ноль.- y Около 6 и 7. Л 210 лет — После■ 9 10 Л Одиннадцать. Считанные секунды Двенадцать. Результаты расчетов сведены в таблицу. 11. Т а б л и Ц А11 * Х®х точек, cm3x п T43T-м Шесть. Ноль. 0 1,000 10,5 2,625 5 210 2,1 — 0,1675 10,5 -0,440 7 417 4.17 0.0052 10.5 0.0137 4 420 4.20 0.0057 10.5 0.0150 8 627 627 0,0019 10,5 0,0050 9 837 8,37 0,0000 — 10,5 0,0000 3 860 8,60 — 10,5 — 2 1070 10,70 — 10,5 — 10 1277 12,77 — 10,5 — 1 1280 12,80 — 10,5 — И 1487 14.87-10.5 — 12 1697 16,97 — 10,5 — М=2.2187 т-м Момент поперечного сечения рельса под нагрузкой точки 6 равен сумме моментов,
вызванных всеми нагрузками, м в-2,2187 т-м.. Как видно из таблицы, момент от нагрузки, приложенной на расстоянии более 8 м от сечения точки, очень мал, поэтому его можно игнорировать в расчетах. 337, максимальное нормальное напряжение в поперечном сечении определяется по формуле Т’ ° 2,2187-10* Триста шестьдесят три =610KP СМ?.
Смотрите также:

