Деформации при кручении стержней круглого (кольцевого) сечений
Для определения углов закручивания стержней круглого поперечного сечения используем дифференциальное уравнение (248).
Полагаем, что крутящий момент и диаметр стержня на этом участке постоянные. Отсюда имеем
Проинтегрируем левую и правую части уравнения (253)
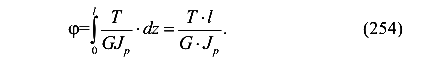
В результате получена формула для угла закручивания участка стержня круглого или кольцевого поперечного сечения постоянной жесткости и постоянным крутящим моментом
где
- Т— крутящий момент на участке стержня;
- l — длина участка стержня; G — модуль сдвига;
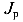— полярный момент инерции поперечного сечения;
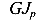— жесткость стержня при кручении.
Полученная формула называется законом Гука при кручении.
Иногда в расчетах требуется найти относительный угол закручивания, то есть угол закручивания, приходящийся на один метр длины стержня. Относительный угол закручивания равен
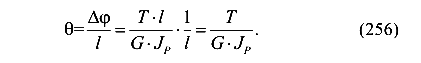
Окончательно имеем формулу для относительного угла закручивания стержня круглого или кольцевого сечений
Эта теория взята со страницы подробного решения задач по предмету «Сопротивление материалов»:
Решение задач по сопротивлению материалов
Дополнительные страницы которые вам будут полезны:
