Оглавление:
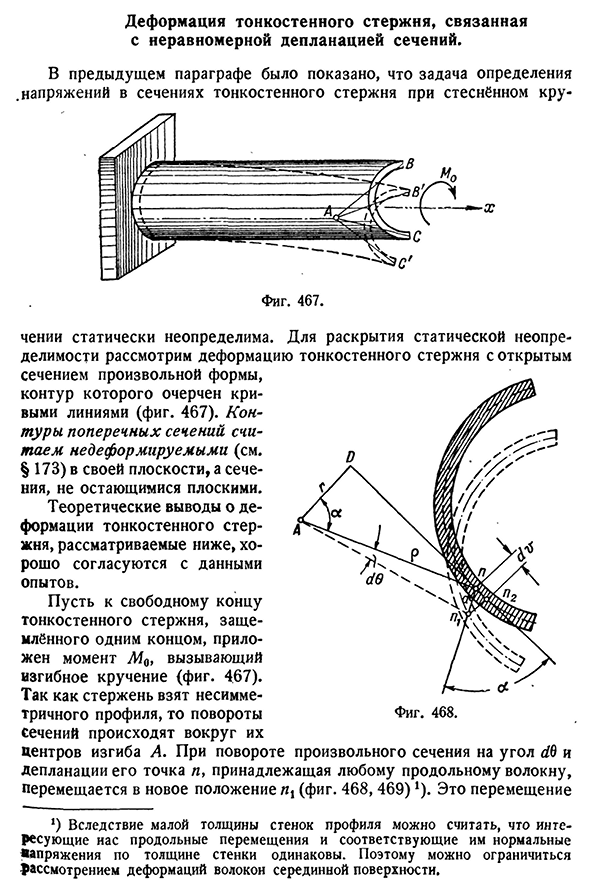




Деформация тонкостенного стержня, связанная с неравномерной депланацией сечений
- Деформация тонкостенного стержня, связанная с неравномерным истощением сечения, в предыдущем пункте указывала на проблему определения. Напряжение в поперечном сечении узких и тонкостенных стержней- Фигура. Четыреста шестьдесят семь chenii является статически неопределимой. Чтобы выявить статическую неопределенность, рассмотрим деформацию тонкостенного стержня с открытым поперечным сечением любой формы и очертим его
контур кривой (рис. 467). Профиль поперечного сечения считается недеформируемым (см.§ 173) в своей плоскости, и поперечное сечение не является плоским. Теоретические результаты по деформации тонкостенных стержней, рассмотренные ниже, хорошо согласуются с экспериментальными данными. На мгновение приложите l40 к свободному концу тонкостенного стержня на одном конце, чтобы вызвать изгиб и скручивание (рис. 467).
Так как стержень взят несимметричного профиля, то поворот сечения происходит вокруг Людмила Фирмаль
их Центра изгиба A (468, 469) x) при любом сечении с углом Yb. Это смещение x) из-за тонкой толщины стенок профиля можно предположить, что интересующие продольные перемещения и соответствующие вертикальные напряжения вдоль толщины стенки одинаковы. Поэтому можно ограничиться рассмотрением деформации волокон промежуточной плоскости.538 основа[гл. XXX Это можно считать состоящим из трех составляющих: одна-точка I, (l-
LA), вдоль касательной средней линии части, вторая-вдоль изделия (468 невидимых перпендикулярно плоскости рисунка) и третья-перпендикулярно L2-p-последняя ищет удлинение волокна (вдоль материнской линии), связанное с обеднением находящегося там волокна. Сначала мы определяем касательную составляющую смещения (I—L4), а затем определяем вертикальное направление, которое может быть связано с касательной. Для определения
- касательной составляющей смещения используют гипотезу о недеформируемости профиля профиля. На основании этой гипотезы, при определении движения касательных в плоскости интервала, необходимо перевести движение интервала в новое положение, лежащее в плоскости 468 и 469) участков изгиба, центрированных по центру жесткого диска. Ограничимся рассмотрением вращения на бесконечно малый угол<Z0, schifig. Разнесенный на расстояние 469 dx, расплавьте его на угол поворота относительно другого участка, примыкающего к нему. При этом вращении точка p равна—a= = pd0, что описывает радиус R-дуги p. Опустив вертикальный r-AD из точки A В продолжение
касательной lo, получим в Вершине a угол, равный углу между сторонами n-и n-Nтреугольника n^PP. Переместить n-касательную на равную ДВ = потому что. Имея в виду R=p cos a, мы получаем dv=p d0cos a=g d9. (30.5) перейдем к нахождению продольной направленной составляющей смещения, указывающей du. Рассмотрим два бесконечно близких участка BC и DE с расстоянием между ними. 469). Поверните сечение ВС относительно Дэ на определенный угол d0, и когда точка перехода n нового положения формирования КН будет равна углу y, видимому из чертежа, dv de dx d d d x’ Знак минус обозначает отрицательное направление угла d9 (при рассмотрении от начала координат вдоль оси x-против часовой стрелки§ 174] деформации тонкого стержня 539
Стрелка) соответствует положительному углу y (по часовой стрелке, если смотреть от полюсов вдоль радиуса g), и наоборот(рис. 469-470). Людмила Фирмаль
Выделим на средней поверхности стержня вблизи одного базового квадрата n точек, стороны которых являются элементами дуги ds(рис. 470). Исходя из гипотезы об отсутствии сдвига на промежуточной грани квадрата при перемещении точки n в новое положение, квадрат не будет искажен, а его прямой угол будет прямым, по которому элемент дуги DS выйдет из плоскости поперечного сечения. Нижний край элемента DS смещается вдоль оси стержня, по величине, для верхнего: du=ds * sin при ds * Y. Подставляя смещение Y: его значение, находим основное продольное- дю= — ДС Общее смещение, накопленное как сумма смещений на базовом сегменте ds, выглядит следующим образом 3 0-6. Пять. И= Здесь g опускается в направлении, перпендикулярном касательной
к средней линии детали, проведенной через точку задачи p от центра изгиба A. 471), что произведение rds равно площади сгиба основания ds и заштрихованного треугольника Ankx, который обозначим d<o=2 * PL. * Д АП/^. Суммируя эти элементарные области длины, я даю площадь дважды: Четыре. Фигура. 471. Дуга$- (30.7) Эта область называется векторной областью или векторной координатой точки n, которая соответствует дуге длины$ и отсчитывается от главной нулевой точки, А веерообразная область различных сечений базиса sho=O 540[CH. XXX Уравнение (30.6)замените интегралами площади сектора, чтобы найти полное смещение по длине точки l, связанной с участком дараматии: «=(30.8) Из Формулы (30.8) видно, что величина продольного направления смещения точки n пропорциональна ее секторным координатам Yu. Таким образом, регион сектора является мерой истощения ран -. Видимый раздел. По длине стер
жня отслаивание зависит от относительно малого угла кручения, теперь можно найти удлинение волокна TP, длину DX(рис. 472). При скручивании стержня точка p перемещается вдоль оси, а при неравном истощении соседних участков расстояние между точками N и t от нее на расстоянии dx, следовательно, расстояние между точками n и t изменяется на величину, равную протяженности линии dx&dx=Ui-11=du-db поскольку n I= — g d e W o t x независим, а 0 является функцией только одной переменной x, расширение волокна выглядит следующим образом __k d x d u d^E dx dx dx2 и l и e= — <o9». (30.9) считает, что волокна друг друга не являются нормальными законами изменения напряжения по закону Гука: Нажмите x), мы можем най
ти в разделе, используя ash== — £<O8″. (30.10) следовательно, величина нормального напряжения при ограниченном кручении зависит от второй производной угла кручения x и следует закону секторной области. Поэтому эти напряжения называются секторными нормальными напряжениями. Общепринятая гипотеза плоского поперечного сечения в процессе сопротивления материала может рассматриваться как частный случай гипотезы секторной площади. * ) Эта гипотеза V. 3. Власов не вошел, поэтому результаты он получил- Е H=Et= — j вместо модуля E——-* •
Смотрите также:

