Оглавление:






Деформации при растяжении и сжатии. Закон Гука
- Напряжение под напряжением и сжатием. Закон крючка. Для того чтобы полностью понять работу растянутых или сжатых элементов, необходимо рассчитать, как изменяются их размеры. Эти же эксперименты позволяют изучить прочность материала, определить его прочность на растяжение и другие характеристики (Глава 11). Для проведения подобных экспериментов в лаборатории используются специальные машины, позволяющие деформировать и разрушать образцы, а также для усилий, необходимых для этого. При этом с помощью достаточно точных измерительных приборов (тензометрических датчиков) мы измеряем деформацию образца.
С помощью тестовой машины теперь можно проводить и точные измерения, конечная нагрузка достаточно велика. Испытательный пресс, который может быть испытан на сжатие всей части конструкции (колонны, части стены), составляет до 5000 тонн; когда дело доходит до испытания на растяжение, лаборатория использует растягивающее усилие до 1500 в большинстве современных лабораторий, натяжение 5-100 тонн и сжатие 200-500 тонн, меньшее усилие. Подробное описание таких машин и устройств, в частности, самой известной российской машины-
Гагаринского пресса, представлено в нашей книге»лабораторные исследования по сопротивлению материалов»и наиболее известных из них. Людмила Фирмаль
Использование таких механических устройств позволяет определить, как изменяется размер образца материала при растяжении и сжатии. Наблюдая, как изменяется расстояние I между двумя точками A и B(рис. 8) Когда вы растягиваете образец, вы можете видеть, что по мере увеличения нагрузки расстояние между намеченными точками увеличивается.§ 8] деформация растяжения и сжатия 33 В таблице 1 показан один из экспериментов, проведенных в машинной лаборатории Ленинградского института инженеров путей сообщения, с отрезанными от рельсов брусками, длиной между двумя намеченными точками. Кроме того, эта нагрузка увеличивалась
ступенчато даже на 0,5 т с каждым увеличением изменения нагрузки Фигура. 8. Приращение длины I (100 мм)между намеченными точками выполнялось специальным прецизионным прибором, называемым тензометрическим датчиком. Так, например, при увеличении 1,5-2,0 Т эта длина увеличивается на величину этих приращений, которые указаны в Таблице 1 на каждом этапе нагружения. Т АБ л и Ц А1. Экспериментальные данные. Тонн груза Расширение от каждого этапа нагрузки ’1000′ * * 1000 м м полное расширение Тонн груза Относительное удлинение от°T o b G в каждой фазе нагрузки * * 1000 м м полное расширение 0.5 1.0 1.5 2.0 2.5 3,0 3.5 4,0 4.5 14.5 14.5 4.5 5.0 5.5 6,0 6.5 7.0 7.5 8.0 8.5 13.7 123.4 13.7 13.6 28.2
- 137.0 13.4 14.4 41.6 151.4 13.5 55.1 14.6 166.0 13.7 68.8 17.5 183.5 13.4 82.2 36.3 219.8 13.6 95.8 328.2 548.0 13.9 109.7 361.0 909.0 П Р и М е ч а н и Е. расчетная длина I = 100 мм. поперечное сечение F=191,2 м2. Рассматривая эту таблицу, мы видим, что: 1) в начале эксперимента увеличение длины пропорционально увеличению нагрузки, и каждое приращение нагрузки на 0,5 т примерно такое же(как и в эксперименте). Если графически представить результаты, полученные в этом эксперименте, то отложим нагрузку в вертикальном направлении и удлиним соответствующую- Беляева давление и деформация при растяжении и сжатии [гл. II Если сечение АВ горизонтально, то в известных пределах (в данном сл
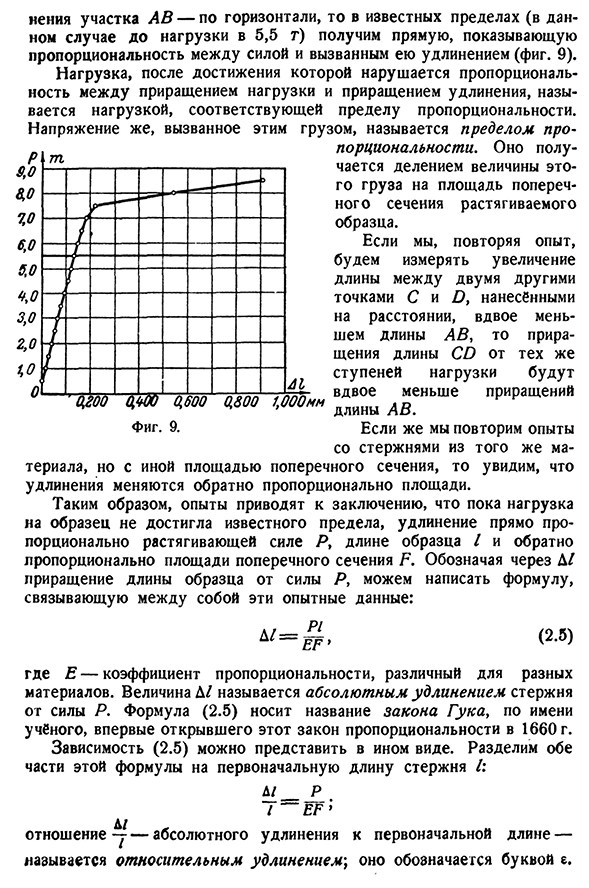
учае до нагрузки 5,5 т) прямая линия указывает на пропорциональность между силой и вызванным ею удлинением.9). Нагрузка после достижения пропорциональности между приращением нагрузки и приращением удлинения называется нагрузкой, соответствующей пределу пропорциональности. Напряжение, вызванное этим 0/М0, 600, 0,800, 1000 мм Фигура. 9. Ага. Иди. Нагрузка называется пределом пропорциональности. Величина этой нагрузки делится на площадь поперечного сечения растянутого образца. Если, повторяя эксперимент, мы измерим увеличение длины между двумя другими точками C и D, построенными на расстоянии AB, равном половине длины CD от того же шага нагрузки.
Повторите эксперимент со стержнем из того же материала, но если поперечные сечения Людмила Фирмаль
разные, то можно увидеть, что удлинение изменяется обратно пропорционально площади. Таким образом, эксперимент приводит к выводу, что относительное удлинение прямо пропорционально растягивающей силе Р, пока нагрузка на образец не достигла определенного предела, длины образца I и длины отбраковки.: ЗАПРЕТНЫЕ ЗОНЫ Ее.* (2.5) Где е-коэффициент пропорциональности, зависящий от различных материалов. Величина D / стержня og силы R называется абсолютным удлинением. Формула (2.5) называется законом Гука, в честь ученого, который впервые открыл пропорциональный закон в 1660 году. Зависимость (2.5) может быть представлена в другом виде. Разделите обе части этого выражения на исходную длину стержня Z: Д / _j П / ~ФВ; Отношение y-абсолютного удлинения к исходной длине-называется удлинением, это буква
E. It обозначается§.§ 8] деформация при растяжении и сжатии 35 Удлинение-это абстрактная величина, отношение двух длин AZ и Z, число которых равно удлинению каждой единицы длины стержня. Перед назначением -. вместо уравнения д/р Шуйского есть значение е, а у значение нормального напряжения, и получается другое уравнение закона крюка: «= — £ — (2-6) Или а=она. (2.7), следовательно, нормальное напряжение растяжения или сжатия прямо пропорционально удлинению или укорочению стержня. Коэффициент пропорциональности материала, который коррелирует нормальное напряжение с удлинением, называется модулем упругости
материала. Чем больше это значение, тем меньше удлиняется стержень, остальные равны (длина, площадь, сила Р). Таким образом, физический модуль упругости е характеризует сопротивление материала упругой деформации при растяжении. Удлинение е-это абстрактная величина, поэтому из Формулы (2.7) коэффициент выражается в единицах, равных напряжению а, то есть единице силы, деленной на единицу площади. Для стали величина этого коэффициента может быть рассчитана с использованием результатов экспериментов, приведенных в Таблице 1. Среднее удлинение образца против пропорционального нарушения от нагрузки 0,5 г равно 0,0136 мм, длина Z равна 100 мм, и, наконец, площадь/7 равна 191,2 м.): Е=—Л МФ’ Назначают P=500 кг, 1=100 мм,
AZ=0,0136 мм, G=191,2 м м \ . E=5 0 0 ′ 19 200 кг] мм — 1 920 000 кг) см. Заметим, что значение модуля упругости материала е не является постоянным, даже если это один и тот же материал, но несколько изменяется. В одних материалах величина модуля одинакова как при растяжении, так и при сжатии(сталь, медь), в других случаях она различна для каждого из этих вариантов. В обычном расчете эта разница игнорируется и принимается для большинства материалов с одинаковым значением E как при растяжении, так и при сжатии. Давление и напряжение растяжения и сжатия[2*36 по гл. Я Следует иметь в виду, что закон крюка выражается только формулами, приближающими результаты эксперимента. Все материалы при растяжении или сжатии дают величину деформации, более или менее отклоняющуюся от этого закона. В некоторых материалах
(большинство металлов) эти отклонения незначительны и могут рассматриваться как полностью пропорциональные зависимости между деформацией и нагрузкой. Однако в практических целях небольшие отклонения от наблюдаемых формул (2.5) и (2.6) можно игнорировать и использовать их при расчете деформации стержня. Среднее значение модуля E для некоторых материалов приведено в таблице 2.It отдается в руки. Более подробную информацию можно найти на последней таблице книги. Т а б л и Ц А2. Величина модуля упругости. Наименование материала Е Миллионы долларов. K2IC1& Сталь…………………………………………………………………. Чугун(серый, б
е л ы м)………………………………………. Медь и ее сплавы (латунь, б / у)………………. Алюминий и дюралюминий…………………………………… Кладка: гр и Н И та………………………………………….. > Из известняка.。………………………………….. > Из кирпича…………………………………………. Бетон…………………………………………………………………. Древесина: вдоль волокон……………………………………. Через волокно………………………………. Резинка………………………………………………………………. Целлулоид. ………………………………………………………… 2.0 1,15 4-1, 60 1.0 0.7 0.09 0.06 0.03 4 0,10-0,30 0.1 0.005 0.00008 0.0193 4-0, 0174
Смотрите также:
| Вычисление напряжений по площадкам, перпендикулярным к оси стержня | Коэффициент поперечной деформации |
| Допускаемые напряжения. Подбор сечений | Примеры |

