Оглавление:




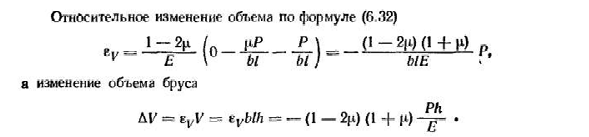

Деформации при объемном напряженном состоянии. обобщенный закон гука
- Объемная деформация Я нервничаю. Закон обобщенных крючков Исследуется деформация и рассматривается проблема долговечности в объемном и плоском напряженных состояниях, изучается основная гипотеза и гипотеза о том, что материал следует закону крюка и деформация мала. Изучая простое растяжение-сжатие, мы можем вычислить относительную продольную деформацию e=■£ ’ (6.27)
И относительная поперечная деформация О, Эти два уравнения представляют закон крюка (отношение между деформацией и напряжением) при простом растяжении или сжатии, то есть при линейном напряжении. Здесь мы установим Зависимость между деформацией и напряжением в общем случае 17$трехмерное напряженное состояние. Закон обобщенного крюка.
Рассмотрим деформацию элемента тела / выберем этот элемент в качестве Людмила Фирмаль
размера A X b x C прямоугольного параллелепипеда(рис. 167). Существует основное напряжение на плоскости параллелепипеда) (C+Yes)= = a&C(1 + ^ ) (1 + 4 ^ ) = Vod+8′) 0+e*>0+ez) = GO (1 + £1+£2+e z+e1E2 ″ G®2E3+£1+V^ZEZ). Учитывая малую величину относительной деформации, последние четыре члена можно игнорировать. Тогда относительное изменение объема V_y= — p — — — — =4-E2+e z-g o, представляющее собой основное растяжение по главному
напряжению по главному напряжению с использованием уравнения (6.29) (6.32) 177в удельный, равномерный при всестороннем сжатии, когда=~0>2=O3= — P, П Куда? Керр. ———— з(1 — Д • Значение/<называется модулем объема. Из Формулы (6.32)、 (6.33)) Под деформатором материал с коэффициентом Пуассона Р==0,5 (например, резина) не изменяется по объему. Я г Ох. Я г Пример 18.
- Балка прочная, но равномерно распределенная по горизонтальной плоскости фигуры (сила Р без натяжения вставляется между двумя неподвижными стенками и подвергается сжатию. 168). Не обращая внимания на трение между балкой и стенкой, найдите силу давления на стенку и измените ее размер, если известны Е и Р материала балки. Сжимающее напряжение, возникающее в продольном
направлении, является следствием эффекта Пуассона и ограничения деформации, то есть вторичным эффектом, вызванным действием напряжения в вертикальном направлении. Поэтому мы предполагаем, что они меньше по размеру, чем вертикальные. В связи с этим введем обозначения напряжений, показанные на рисунке. 168 (т в торце штанги явно отсутствует, поэтому именно они будут основным напряжением). Тогда иметь
С помощью N указывается давление на стенку стержня. Размер/не изменяется Людмила Фирмаль
в зависимости от условий задачи, поэтому E2=0. Из второго уравнения(6.29)= — g—(O2-DPC)=0, То есть Значение, ППГ В дальнейшем, АВ=ЭГ ВР е (О2+О3) И(М-Р) Р Е1♦ Ах=e8h= Д Е (П3| / П2)=—(1-Р2) РН кости 178 минут W Относительное изменение объема по формуле (6.32)) Один. —. ми= — Изменение объема пучка Р(1-2ч) (1+н) о бл я~з>
Смотрите также:
| Обратная задача в плоском напряженном состоянии | Потенциальная энергия деформации |
| Понятие об объемном напряженном состоянии | Задачи теорий прочности |

