Оглавление:




Деформации кривых стержней
- Варианты криволинейных стержней Деформационные стержни общего случая плоского изгиба (M=f=0, N f0, Q4*0) представлены: M4s, F Jvm, G MNds, p Q2ds J2EFep+J2EF+J2EF + J EFp+J2GF С ч С С С с (7-12) Здесь M, N и Q-текущие значения внутренних сил, знак которых вводится в Формулу (7.12), где k-коэффициент, зависящий от формы
поперечного сечения. Для прямоугольного поперечного сечения k=1,2; для круглого k=1,1;для двутавровой балки fe=-p-(F поперечное сечение двутавровой балки; FCT площадь стенки двутавровой балки),
l и G—для продольной упругости и сдвига соответственно. В Формуле (7.12) Людмила Фирмаль
Интеграл распространяется на всю длину луча. Если Интеграл IME С Рис. Если длина s имеет разрывы, то Интеграл выполняется на графике, и соответствующие члены в Формуле (7.12) представляются как сумма интегралов на графике. Расчет смещения. Для плоских криволинейных балок с большой кривизной линейные
и угловые перемещения определяются по формуле Мора: C MMds, C NNds, G (MN+NM)ds, t f QQds J EFep EFP GF Ы ы ы ы ы ы ы (7.13) Где M, N и Q-текущие значения внутренних сил от заданной нагрузки, M, N и Q-единичные линейные перемещения, которые прикладываются к точке, где перемещение определяется в направлении искомого
- перемещения, соответствует единичной сосредоточенной силе, а угол-единичной паре. Интеграл (7.13) простирается по всей длине балки. Если Интеграл берется в разрезе, то общая длина стержня соответствует сумме интегралов. В случае криволинейной балки с малой кривизной (R>5) можно найти движение без учета кривизны:
С Продленным доступом ЭИ’ (7-и) Где 1-момент инерции сечения относительно центральной оси, параллельной нейтральному слою. Если смещение, рассчитанное по формулам (7.13) или(7.14),
оказывается отрицательным, то оно направляется в направлении, Людмила Фирмаль
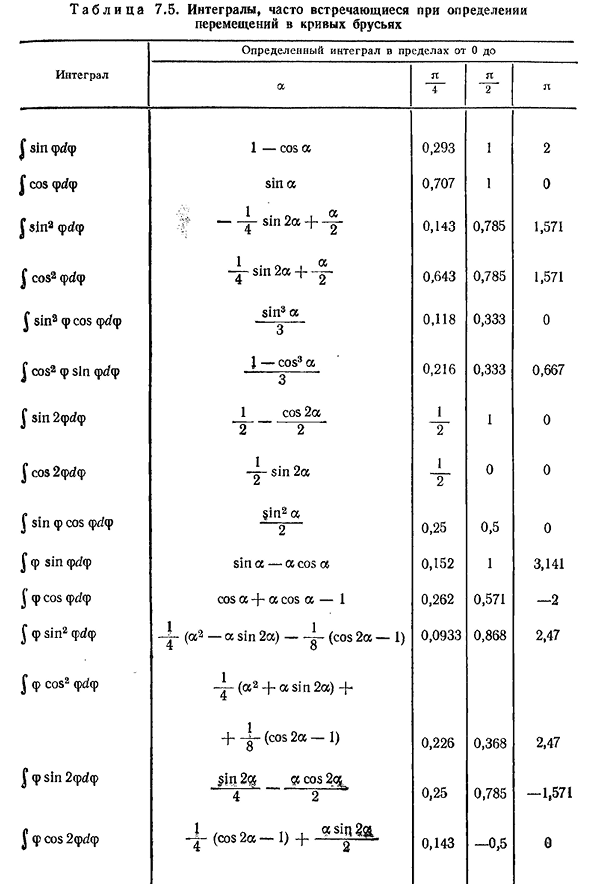
противоположном принятому направлению установки на столе. Приведены значения интегралов, которые часто встречаются при определении перемещений по формулам (7.13) и (7.14). Стол. 7.6 включает в себя максимальное смещение и максимальный изгибающий момент некоторых изогнутых стержней. 178T а б л и Ц А7. 5. Интегралы часто встречаются при определении кривой
смещения пучка Неотъемлемый Определенный интеграл в диапазоне от 0 до 0 Но Л / грех FYF1-cos0, 293 1 2И постепенно росла, потому что грех А0, 707 1 0|sin2FS/ф-г-4 грех 2А+ 2 0,143 0,785 1,571 Джей COS2FS/f4s м2а+ 2 0,643 0,785 1,571 Дж sin2f потому что / ф грех ® А3 0.118 0.333 0 Дж COS2f грех Ф(1F1-сов®А3 0,216 0,333 0,667 Джей грех 2fs по / f1cos2A2 2 Один. — Т. Один. Ноль. Дж cos2fyf грех 2A1 Два. Ноль. Ноль.
sinf по потому что постепенно росла §in2a2 0.25, 0.5, 0. Х |ф грех грехом постепенно росла а-значение COS А0, 152 1 3,141 Дж. Ф. косе ФС/Ф в COS а+а потому что— 1 0,262 0,571 −2 И. Ф. sin2FYF(А2-грех 2а)—— 1- (cos2A-1) 0.0933 0.868 2.47/Ф COS2FB / ф-я — (2+грех 2А) — Дж- +(cos2A-1) 0,226 0,368 2,47 Дж. Ф.$!p2fs / p sin2$ » cos2q^4 2 0.25 0.785 — £Ф cos2far я(cos2a1)+ — £ £ ^п0. 143-0. 5 0 179T а б л и Ц А7. 6. Максимальный изгибающий момент и смещение криволинейных стержней Тип изогнутого луча^перемещение D Макс Икс Ма=РР при вертикальном
перемещении сечения-РР3 в НИИ; а-0,785;при горизонтальном перемещении сечения-РРА ния: а-0,5 е j Но L1a = = = PP горизонтальная секция перемещения—R(>3 НИА Б:= £ 0.356 Дж В сечении l4a=2rr вертикальное смещение-PP3NII: A-0,471 E j L1C в разрезе=PP горизонтальное перемещение-PP3niya B: A-1,571 E j P MA=p (p+1)сходимость концевого участка:■ х(4Z2+в Р2+2z паза п ) ] I ma=2pr сходимость в выходном сечении: P3A-9.42 E J >д л£ фа МА=0.318 ПП МВ—0.182 ПП Диаметр изменения: вертикальный- PP3nogo а-0,149 Э J; горизонт- PP3t-А——0,137 — Для 180 случаев определяют горизонтальное перемещение точек на оси изогнутой балки.
Показано на фиг. 7.7 если=1. Балка прямоугольного сечения h X B; k= = = 1,2; G=0,4£. Третий член Фомула (7.13) может быть проигнорирован. Решение. Запишите формулу M, N, G внешней нагрузки, заданной для текущего поперечного сечения криволинейной балки: М= — ПП греха<п; п=п грех<р; д-р соѕ Ф. Нагрузите балку удельной силой Р=1. 7.7, b), применить горизонтально к точке b (в направлении желаемого движения). Запишите выражение силы в единичном состоянии нагрузки: M= — p sin f; W=sin f; Q = cos f. DS=RUF; при интегрировании по всей длине стержня он подставляет формулу
нахождения внутренних сил в Формулу (7.13), имея в виду, что она определяет искомое перемещение.: х EFep ПП грех грех фр фр постепенно росла п ф грех грехом fryf эф +1.2 х L R COS f COS fryf Pp2l ((UDE~2EFe’ Отчет РРА, Rrrl_lrrr/Р\2EF+2EF~2е Ф\э Значение конкретного интеграла берется из таблицы. Это 7.5-г=1е=0.0897 ч, р ч ч — =-=»qqggytt-Н, 14. Подставляя полученное соотношение в Формулу смещения, получаем, наконец.: И= LRR~2EF (11,14 + 1 + 3 )=7.57 вечера ЛРР ЭФ
Смотрите также:

