Оглавление:
Давление жидкости на вертикальную пластинку
По закону Паскаля давление жидкости на горизонтальную пластину равно весу столба этой жидкости, имеющего основанием пластинку, а высотой —- глубину ее погружения от свободной поверхности жидкости, т. е.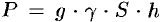 
, где 
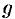— ускорение свободного падения, 
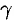— плотность жидкости, 
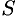— площадь пластинки, 
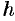— глубина ее погружения.
По этой формуле нельзя искать давление жидкости на вертикально погруженную пластинку, так как ее разные точки лежат на разных глубинах.
Пусть в жидкость погружена вертикально пластина, ограниченная линиям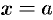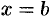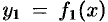и 
, 
, 
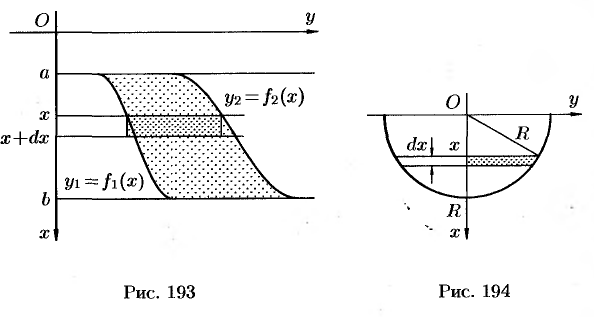
и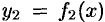 
; система координат выбрана так, как указано на рисунке 193. Для нахождения давления 
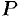жидкости на эту пластину применим схему II (метод дифференциала).
1. Пусть часть искомой величины 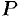есть функция от 
: 
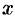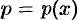, т.е. 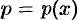— давление на часть пластины, соответствующее отрезку 
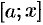значений переменной 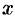, где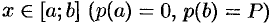 
.
2. Дадим аргументу 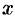приращение 
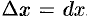. Функция 
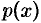получит приращение 
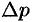(на рисунке — полоска-слой толщины 
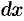). Найдем дифференциал 
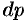этой функции. Ввиду малости 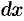будем приближенно считать полоску прямоугольником, все точки которого находятся на одной глубине 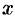, т. е. пластинка эта — горизонтальная.
Тогда по закону Паскаля
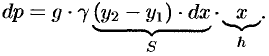
3. Интегрируя полученное равенство в пределах от 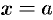до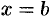
получим
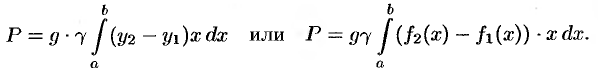
Пример №41.13.
Определить величину давления воды на полу круг, вертикально погруженный в жидкость, если его радиус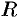 
, а центр 
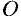находится на свободной поверхности воды (см. рис. 194).
Решение:
Воспользуемся полученной формулой для нахождения давления жидкости на вертикальную пластинку. В данном случае пластинка ограничена линиями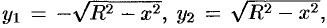 
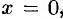
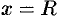. Поэтому
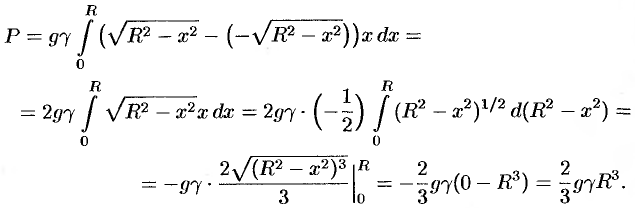
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
