Оглавление:



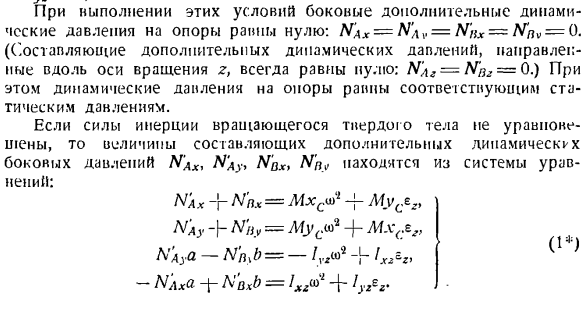






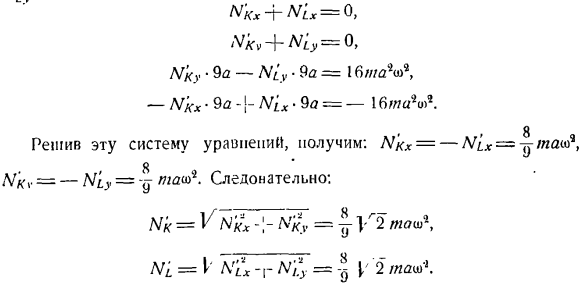


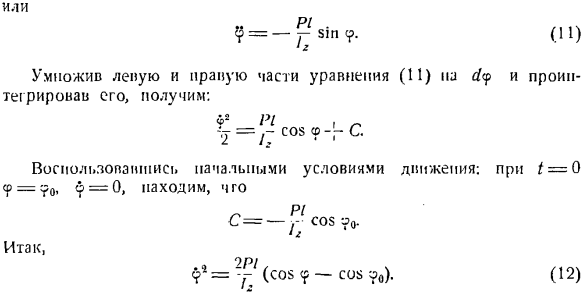
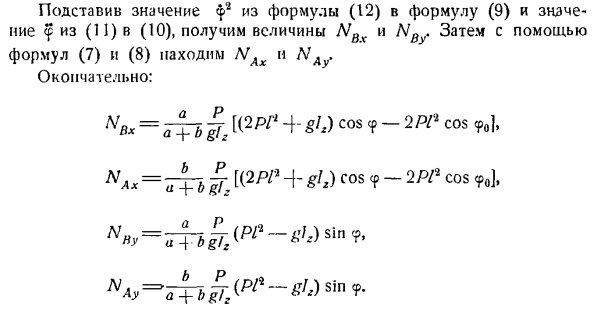







Давление вращающегося твердого тела на ось вращения
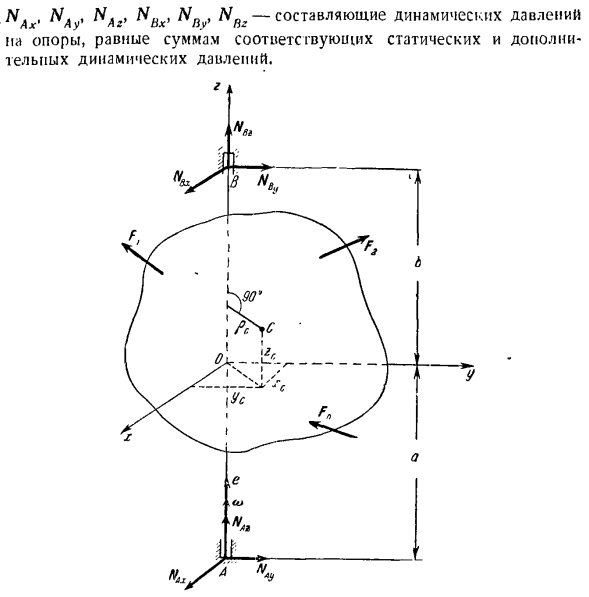
- Давление вращающегося твердого тела на вращающуюся ось Когда твердое тело вращается вокруг неподвижной оси, к твердой опоре прикладывается дополнительное давление. Соединить подвижные оси XYZ на твердое тело(рис. 1512). O-любая точка на оси вращения. ось Z направлена вдоль оси вращения. оси x и y вводятся вместе с осью z для формирования правильной системы осей. M-масса твердого тела, o-угловая скорость твердого тела, g-угловое ускорение
твердого тела, C (xc, yc, zc) — центр тяжести твердого тела, 1xg> 1uz-центробежный момент инерции твердого тела, a, b-расстояние Lu от опоры B до начала координат. Н недорогой, Н А ^ П)\ Х, УСД «* н я- Дополнительные компоненты поддержки па динамического давления. Дополнительное динамическое боковое давление возникает на опорах а и В.\, даже если эксцентрик ПК мал, но угловая скорость w велика. Этот дисбаланс называется статическим, поскольку его можно обнаружить при отсутствии вращения диска. Если ось вращения диска проходит через
Это во много раз превышает соответствующее статическое давление Людмила Фирмаль
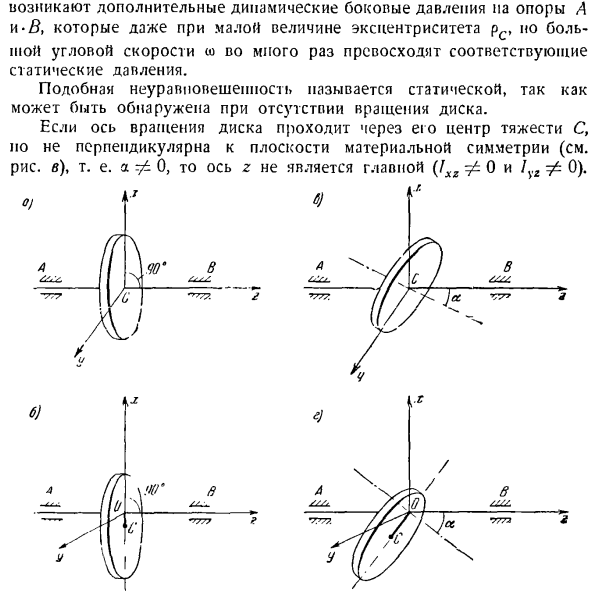
центроид C, то он не перпендикулярен плоскости симметрии материала(см. Рисунок B) (то есть a 0), а ось z не является главной(1xr и 1y2 0). г. В.1-6.) В / ■ Вт «^7?。£77777 4G Л! Кг И Л / / л ч / / ч/. в / о) 1 / — В С / с? — Дж. — я не уверен. ’И Y \ / /’ \ h » 7773K задача 371. В результате вспомогательные моменты силы инерции] не будут равны пуле, и на опору возникнет дополнительное динамическое боковое давление! «А и С. Даже если значение угла и угловой скорости W является большое значение велико. Этот дисбаланс называется динамическим, так как он обнаруживается только при
вращении диска. Практически невозможно подтолкнуть диск к оси вращения крюка так, чтобы он был совместим с осью симметрии, то есть ПК и а не равны пуле (см. Рисунок D).в результате основной вектор и вспомогательный момент инерции не равны пуле, а на опоре а возникает дополнительное динамическое боковое давление, которое значительно больше соответствующего статического давления. Проблема устранения дополнительного динамического давления играет огромную роль в современной технике. Это неудивительно, поскольку в конструкции двигателя и производственной машины обычно имеется неподвижная ось (Ротор диска турбины,
- электродвигатель или генератор, деталь, вращающаяся с высокой угловой скоростью).Например, шпиндель токарного или расточного станка). Задача 372.Определите дополнительное динамическое давление, оказываемое на подшипники K и L на коленчатый вал конструкции, описанной в задании 312.Вал вращается с постоянной угловой скоростью. Решение. Координаты центра тяжести вала определяются по формуле (см. рисунок в задании 312). налог A + mDXt)+ tex E + txp tL -\ -! Б + Мб + МД = телевидение.2а + т0 (- 2а)= Щ ма-\ — МН + я + МД = I mkyb _ * aUa + mflynn + mdyf+ mdyn _ jj1mama + MB + me + MD Тэ тп-2а + (- 2а) — ма + МВ + Мб + МД〜 (напомним, что xA = x£= yn = yn = 0). . Этот результат и задача 312: lvz = / x2 = r-1
используя значение момента центробежной инерции, рассчитанное с помощью Gma4, построим систему уравнений (1*) для определения прогноза дополнительного динамического бокового давления N’KX, N’KV> N’x’. \ ч Ф9 * к Г ’/ Л 。 _E ГП \ колледжа С — £ ТК Н-КХ + MLX По = Скорострельный <Vicv + Улы = 0、 Y’Ku•9 <2-N [y-9a = l 6w * V, — N’KX = — 16w » V. Восемь После решения этой системы уравнений она выглядит так: N’KX = — Afix = — U thai? г Н-кВ =-А ^ = — Г niao)4.В результате: Г = = \ 1МА * \ Ni = l a£ — yn / * y = J I 2 / W Дополнительное динамическое боковое давление вращается вместе с твердым телом. Они образую
Поэтому центр тяжести c коленчатого вала находится на оси Z Людмила Фирмаль
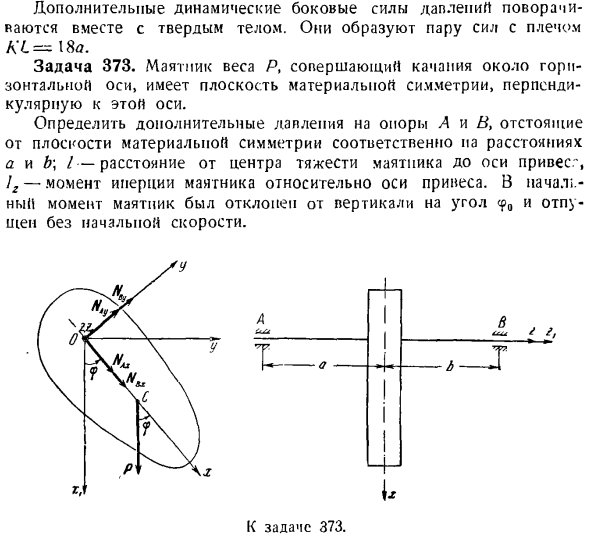
т силу 1 пары при плече LH = 1. Задача 373.Маятник со своим весом P, который качается вокруг горизонтальной оси, имеет материальную плоскость симметрии, перпендикулярную этой оси. Расстояние a и b соответственно от материала симметрично плоскости для определения дополнительного давления опор A и B; I-расстояние от центра тяжести маятника до оси веса. 2-Момент инерции маятника относительно оси веса. От вертикального угла cp0 выпускается без начальной скорости. Голы: 373 Решение. Направление выбранной
неподвижной оси xlt ylt zt и подвижной оси x, y, z, связанной с маятником, показано на рисунке. Центроидные координаты маятника равны ХС = /, уя =0.(Я) Так как ось усиления z перпендикулярна плоскости симметрии материала маятника, то она является главной осью инерции на пересечении о с этим plane. So … Кг = Гц-(2) Единственная сила, которая дается, — это вес P маятника. Подшипники носят A и I. So компонент давления вдоль оси Z коэффициента усиления отсутствует: MAG = 0.
Учитывая уравнения(1) и (2), построим систему уравнений (J*) для определения значений составляющих динамического давления. Л. Л * + НН.< = J I? + Р с COS ^ yh «^ lu ‘ tyfc-это компонент динамического давления опоры па, равный сумме соответствующих статических и дополнительных динамических давлений. Построим систему уравнений(2), определяющую величину составляющих динамического давления Па опоре. Л / = Р Унция.— » \ Т п& 9 л а Ay1 = T2£3 ‘ Накса = 0. Поскольку поддержка на подшипник, Н ^ Р = 0. После решения системы уравнений определите искомые значения составляющих
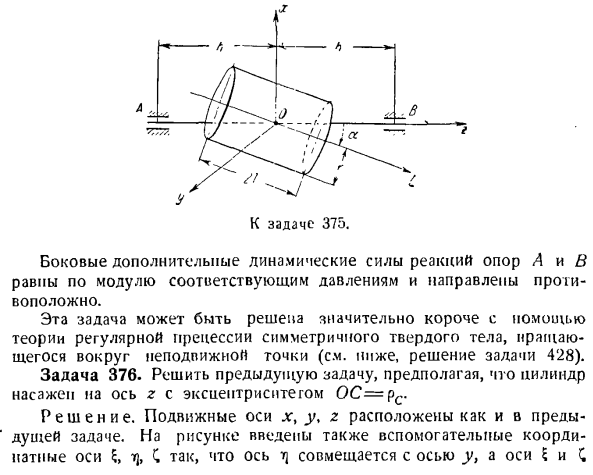
упорного подшипника O и динамического давления пластин на подшипник A. Нет = + ¥ > «о,= Jflu) 9-Ф• При вращении пластины AQB вокруг оси z с постоянной угловой скоростью ω возникает инерционная сила и создается дополнительное давление на опору. Л » = aco9,н ’= ф — зя А в 12 граммах ’ ой 4 грамма Статическое давление пластины на опору равно Л / ст _ Р D7ST-Р Д / С — _ _ Р ОЗ-1 ″ ад-з’о-3 * Задача 375.Прямой, однородный круговой цилиндр с массой P,
радиусом r, длиной 2 вращается с постоянной угловой скоростью вокруг оси z через центр тяжести C. ось вращения цилиндра z образует ось симметрии C, а угол a. для OA-OB-h определяют дополнительное динамическое поперечное давление опор A и B. Панели ir и e. движущиеся оси x, y и z, связанные с цилиндром, показаны на рисунке. Был рассчитан центробежный момент инерции цилиндра и выполнена задача 314. Ноль) Центр тяжести С цилиндра по оси Z 、 ХС = США = °- (2) Цилиндр вращается равномерно、 е =0.
(3) Используя Формулы (1), (2) и (3), построим систему уравнений (1*) для определения величины составляющих дополнительного бокового давления N’Лх, N’Av, N’NX, n’by. + о — +N’NXB == 2-g(?- Джей) грех Когда вы решаете эту систему уравнений, она выглядит так: = = «в,= — Н А,= — Л(С-Т) Си» Айбай » oxax 4gh \ 4 Так, при вращении цилиндра создается дополнительное боковое давление на опоры А и в, образуя пару сил на плече АВ = <2Н. Боковая дополнительная динамическая сила реакции опор а и в направлена в противоположную сторону, абсолютное значение которой равно соответствующему давлению.
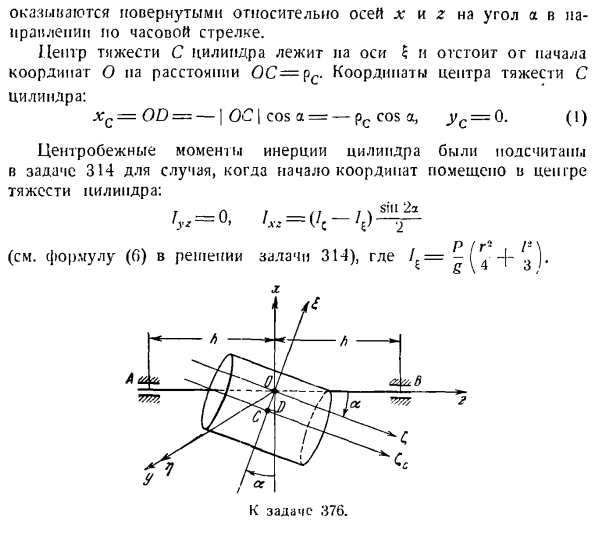
Эту задачу можно решить гораздо короче, используя теорию регулярной прецессии симметричных твердых тел, вращающихся вокруг неподвижных точек (см. Решение задачи 428 ниже). Проблема 376.Решите предыдущую проблему. Предположим, что цилиндр установлен на оси z с эксцентриком OS = pc. Решение. Подвижные оси x, y, z расположены так же, как и в предыдущем задании. Поскольку вспомогательная координатная ось%C также введена на этом рисунке, оси выровнены по оси y и осям. И C
Только угол a по часовой стрелке будет повернут относительно осей x и Z. Центроид c цилиндра находится на оси$и окружен началом координат O на расстоянии OS = pc. Координаты центроида с Цилиндр: ХЖ = ОД = — / ОС | потому что ПК—потому что в США =0.(1) Центробежный момент инерции для цилиндра был рассчитан в задаче 314, когда начало координат было помещено в центр тяжести цилиндра. / «=0, / д,= (/с — / £)〜- п / ДХ [Т] \ (См. формулу (D) решения задачи 314), где I = — i ..это не так. икс Вычислите момент инерции цилиндра вокруг оси С. Центр тяжести c-ось Cc, параллельная оси C,
и Давай сделаем это. Напишите теорему Шгейера: / s = / ss• — так как/ ss-10 И я, / П2, мне * Так… 。 ч. грех 2.1 / / В9, Р О, Р р-р п \ Син 2 * /Л,=(/с -/.) — = + ^ ПК—4—ч) -= П / Т= Л / = \Силл 2а — +ПК-с /- Так… / ,, = 0,/ з =£ф 4 4—к)грех ’ 2а. (2) Цилиндр-это rlsho. to поверните черо、 е =0.(3) Используя Формулы (1), (2) и (3), построим систему уравнений (1*), определяющих значения составляющих дополнительных динамических боковых давлений N’x, N \ N \ v, N’x, N’uy -. Н’а.- ’ .-Н ’ ^
т р ^’ Кост、 — N ’Ji 4-N’ J, — = £(J-Pi—sin 2a. после решения этой системы уравнений можно увидеть следующее: ДГ ’- П> = 0 / с V’ =-^ я; Р — — — Пи-кг, потому что alоД Ай-Пу-у * ’ В Л * С-Л-и (О4. Боковые дополнительные динамические силы реакции опор а и 1)направлены в противоположную от них сторону, абсолютное значение которых равно соответствующему давлению. 152. Эта задача может быть решена методом кинетической статики. Когда мнимая сила инерции
твердого тела подводится к центру О, получается сила, равная силе основного вектора и 1 набору сил, а момент равен основному моменту силы инерции/ i*/». Проекция главного вектора силы инерции твердого тела Тело x} y> z на движущихся осях связано с твердым телом В {ХЈ)= mxc по ^ Mycezi В (Дж] = му(.о > ’ 1-Mxcezt в [Дж] = о Молекулы основного вектора инерционных сил Олрс)= ПДК В » Где pc = yx-c-y’cc-эксцентриситет, то есть расстояние от центра масс твердого тела C до оси вращения. pc = 0, то есть если центроид C твердого тела находится на оси Z вращения, то основной вектор инерции гасится. Основные моменты силы инерции твердого тела для движущихся осей x, y и zy, связанных с твердым телом, описаны в следующем виде: Он вводит другой вспомогательный момент, чем
основной Момент. При отсутствии составляющей основного момента силы инерции относительно оси инерции к центру вращения z. модуль этого момента Момент m {oY будет пулей, если 1xr-1yr = 0, то есть если ось вращения z является главной осью инерции в точке O. Для силы инерции твердого тела, вращающегося вокруг неподвижной оси, уравновесить в смысле V (/)= 0、 После этого, * = 0, необходимо и достаточно, чтобы ось вращения z была главной инерционной осью твердого тела(p = 0, lxz = При этих условиях дополнительное динамическое давление в боковом направлении опоры будет равно нулю: N ’ax = N \ v = N’ hx = N, fiv = 0. 。)В этом
случае динамическое давление опоры будет равно соответствующему статическому давлению. Если инерционная сила вращающихся тел не уравновешена, то из системы уравнений получены значения дополнительного динамического бокового давления N’ax, N’y> N’Dxf N’ny компонентов. Н недорогой-р м’ph = mhsf1-Ф myce2t Н А Г — (- Н’iiy = Afyc <О2-Джей-МХ(п» + N’AYA-N’nyb = — / VX-h°} — NAxd-f-N’AXB = If / a * — f-lyfr Величина динамической составляющей давления NAxt NAv, Nbx> Nnyy Nnz>, определяется из системы уравнений, равной сумме соответствующего статического давления и дополнительного
динамического давления. Н АКС-Р нумераторы nbx = Mxc0)5 + Мускат + х К-Я Ная-НТ> Ыб =-х * + «• »+ 2″ я * Л). АР = 1 — «г,* + = + в + 2(б)> к = I Сила дается Flt Ft, Fn. Из 3-го уравнения (2*) системы, а также соответствующих уравнений статики, можно определить сумму значений составляющих давления NAz и Nqz. Каждый из них не может быть рассчитан индивидуально. Если опора осуществляется в виде Нилина- н Dylick подшипник, то Лгв * = 0, и поэтому Naz = V } Fkz. к-мне Задачи, требующие определения дополнительного динамического давления в боковом направлении опоры, решаются с помощью системы уравнений(1*).
Задачи, необходимые для определения динамики опоры, решаются системой уравнений(2). Задача определения динамического давления вращающегося твердого тела на ось вращения лучше всего решается в следующем порядке: 1) Выберите подвижную ось x, y, z, связанную с вращающимся твердым телом, и укажите ось z вдоль оси вращения(если центр тяжести C находится на оси вращения, то удобно совместить начало координат O и центр тяжести C; если нет начала координат C на оси вращения, то центр тяжести C
находится на оси вращения).); 2) система предварительно подключенного питания показана на рисунке. 3) координаты центра тяжести c твердого тела xc nus \ 4) твердый центробежный момент инерции Ihg и / y / рассчитать、 5) а) если неизвестное значение представляет собой дополнительное динамическое давление в боковом направлении относительно опоры, то оно образует систему уравнений (I). Б) если неизвестной величиной является динамическое давление опоры, создайте систему уравнений (2). 6) решить систему уравнений(1) или(2), а затем определить требуемую величину. Если решается задача определения бокового дополнительного динамического давления на опору, то опуска
ется 2-й пункт, решающий задачу. Задача 371.Равномерный круговой диск вращается вокруг неподвижной оси. Как должна быть расположена ось вращения диска относительно оси симметрии, чтобы дополнительное динамическое давление опоры было равно нулю? Решение. Основной вектор V (J) и вспомогательный, чтобы избежать дополнительного динамического давления на опору Для моментов инерциидолжно быть равно пуле: V (y,= 0、 Тогда ’= 0. (IE) = MPc Y + u = V ^ z-Y ^ z + <тогда _ Если Mrs= 0; I = 0, VHz + 7%. Сумма M
, co и£не равна пуле, поэтому pc = (), fxz = jys = 0, то есть ось вращения z должна быть главной инерционной осью диска. Для выполнения полученных условий необходимо совместить ось вращения диска с его осью вращения symmetry. In дело в том, что ось симметрии однородного кругового диска проходит его центр тяжести, то есть pc = 0, поэтому основной вектор силы инерции V [J) Чтобы zero. In кроме того, ось симметрии диска перпендикулярна плоскости симметрии материала. То есть главная ось инерции на пересечении с этой плоскостью! Xr = fV2 = 0.So, вспомогательная сила инерции равна нулю. Поэтому для того, чтобы дополнительное динамическое
давление на опору было равно пуле, ось вращения диска должна соответствовать его оси симметрии. То есть он должен проходить через центр тяжести диска перпендикулярно плоскости симметрии материала (см. рисунок а). Эксцентриситет ПК не равен нулю, если ось вращения диска z перпендикулярна плоскости симметрии материала xy и не проходит через центр тяжести c диска (см. Рисунок B).Поэтому основной вектор силы инерции V^) не равен zero. At в то же время
Смотрите также:
Предмет теоретическая механика
| Классификация связей. Число степеней свободы. Классификация сил | Принцип возможных перемещений |
| Метод кинетостатики | Общее управление динамики системы материальных точек |

