Курсовая работа К2
Даны уравнения движения точки в плоскости 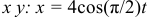
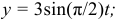 (
(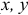 — в сантиметрах,
— в сантиметрах, 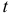 — в секундах).
— в секундах).
Определить уравнение траектории. Построить траекторию, найти положение точки на траектории в момент времени 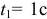 . Вычислить скорость и ускорение, а также касательное, нормальное ускорения точки и радиус кривизны траектории для
. Вычислить скорость и ускорение, а также касательное, нормальное ускорения точки и радиус кривизны траектории для 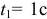 . Изобразить векторы скорости и ускорения, а также касательного и нормального ускорений в заданный момент времени.
. Изобразить векторы скорости и ускорения, а также касательного и нормального ускорений в заданный момент времени.
Решение
- Для определения траектории движения точки из заданных уравнений движения исключим время
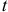 .
.
Учитывая, что под знаком «синуса» и «косинуса» одинаковый угол, воспользуемся формулой
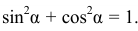
С этой целью из уравнений движения выразим в явном виде эти функции
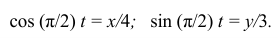
Возведем в квадрат левые и правые части уравнений, затем их сложим. Окончательно получим уравнение траектории
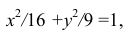
которое является уравнением эллипса с полуосями 4 см; 3 см (прил. 4, рис. К1).
- Найдем положение точки на траектории при
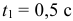 .
.
Чтобы определить положение точки в какой-то момент времени, надо это время подставить в заданные уравнения движения. При 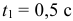
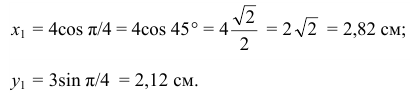
- Определяем скорость точки по проекциям на координатные оси
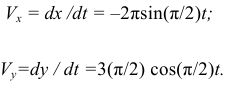
При 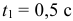
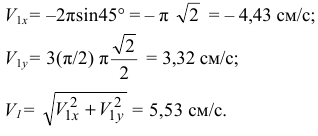
На рисунке 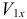 и
и 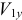 изображаем в масштабе
изображаем в масштабе 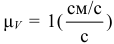 с учетом знака проекций, при этом скорость точки должна быть направлена по касательной к траектории движения точки (см. прил. 4, рис. К1). 4. Определяем ускорение точки по проекциям на координатные оси.
с учетом знака проекций, при этом скорость точки должна быть направлена по касательной к траектории движения точки (см. прил. 4, рис. К1). 4. Определяем ускорение точки по проекциям на координатные оси.
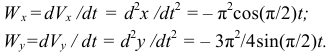
При 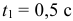
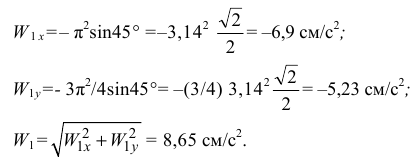
Изображаем 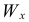 и
и 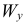 на рис. К1 прил. 4 в масштабе
на рис. К1 прил. 4 в масштабе
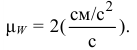
При определении векторов 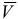 и
и 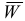 графическим способом надо проекции этих векторов на оси
графическим способом надо проекции этих векторов на оси 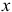 и
и 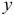 откладывать из точки
откладывать из точки 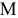 в определенном масштабе, а затем на этих проекциях как на составляющих строить прямоугольники, диагонали которых и будут определять эти векторы (см. прил. 4, рис. К1).
в определенном масштабе, а затем на этих проекциях как на составляющих строить прямоугольники, диагонали которых и будут определять эти векторы (см. прил. 4, рис. К1).
- Определяем касательное и нормальное ускорения.
Касательное ускорение находим по формуле
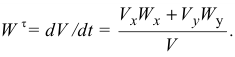
При 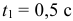
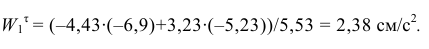
Касательное ускорение направлено как и скорость по касательной к траектории. Касательная ось направляется по касательной к траектории движения точки в сторону положительного отсчета криволинейной координаты. Касательное ускорение получилось положительным. Это означает, что касательное ускорение направленно в ту же сторону, что и скорость 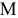 , и точка совершает ускоренное движение
, и точка совершает ускоренное движение
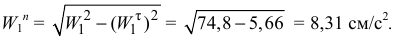
Нормальное ускорение направленно по нормали к траектории движения точки к центру кривизны этой траектории.
- Определяем радиус кривизны траектории в момент времени
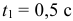
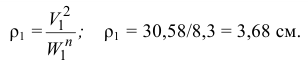
Радиус кривизны 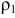 откладываем от точки
откладываем от точки 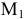 по нормали к траектории.
по нормали к траектории.
При этом находим положение центра кривизны траектории — точку 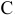 . (см. прил. 4, рис. К1).
. (см. прил. 4, рис. К1).

