Оглавление:

Цилиндрические поверхности
- Цилиндрическая поверхность Поверхность, образованная движением прямой линии L, которая поддерживает постоянное направление и движется в пространстве каждый раз, когда конкретная кривая K пересекается, называется цилиндрической поверхностью или цилиндром. Кривая K называется направляющей цилиндра, а линия L — ее шиной.
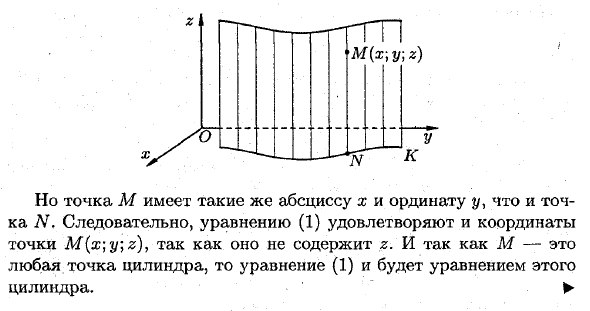
Рассмотрим цилиндрическую поверхность, где направляющая находится в одной из координатных плоскостей, а генератор параллелен координатной оси, перпендикулярной этой плоскости. Поместите линию К на плоскости Оху и (1) F (x; y) = 0.
Постройте цилиндр с генератором, параллельным оси Oz и направляющей К. Людмила Фирмаль
Теорема 1. Уравнение цилиндра, генератор которого параллелен оси Oz, имеет вид (1). То есть он не включает координату z. <4 Возьмем цилиндр с произвольной точкой M (x \ y \ z). Она лжет в нескольких формах. Пусть N будет пересечением этого генератора и плоскости Оху. Следовательно, точка N находится на кривой K, а ее координаты удовлетворяют уравнению (1).
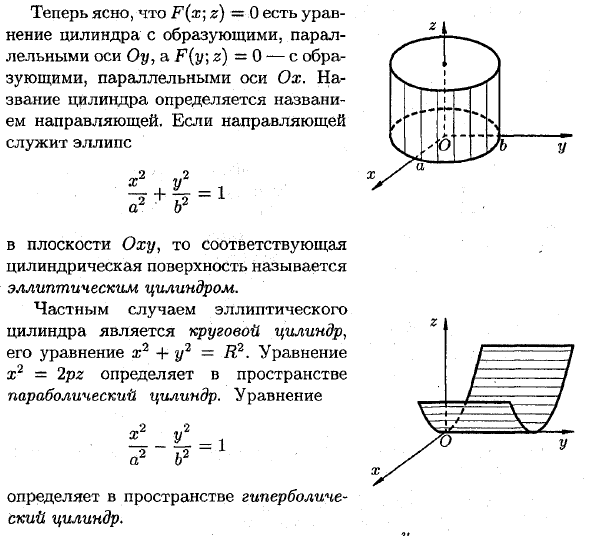
Однако точка M имеет ту же абсциссу x и ординату y, что и точка N. Следовательно, координата (x; y7z) 1 точки M не содержит z, поэтому она удовлетворяет уравнению (1). Кроме того, поскольку M — произвольная точка на цилиндре, уравнение (1) является уравнением для этого цилиндра. ► GGP M (x \ y \ z)Теперь ясно, что F (x; z) = 0 является уравнением для цилиндра с генератором, параллельным оси Oy, и что существует генератор, параллельный оси F (y; z) = 0-Ox.
| Прямая линия в пространстве. Основные задачи | Поверхности вращения, конические поверхности |
| Прямая и плоскость в пространстве. Основные задачи | Канонические уравнения поверхностей второго порядка |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Название цилиндра определяется по названию гида. Когда гидом является эллипс 2 2 — + £ = 1 a2 ‘b’2 В плоскости Оху соответствующая цилиндрическая поверхность называется эллиптическим цилиндром. Частным случаем эллиптического цилиндра является цилиндр с уравнением x2 + y2 = R2. Уравнение x2 = 2pz определяет параболический цилиндр в пространстве. уравнение a2 b2 ~
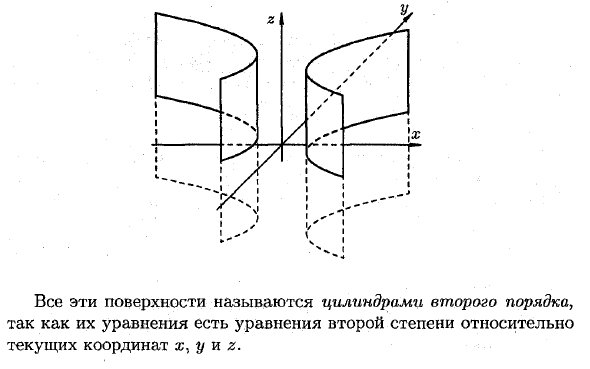
Все эти поверхности называются квадратичными цилиндрами, потому что они представляют собой квадратные уравнения для текущих координат от x ^ y до z.
Определить гиперболический цилиндр в пространстве. Людмила Фирмаль

