Оглавление:
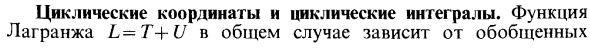





Циклические координаты и циклические интегралы
- Функция Лагранжа L = T + U в общем случае обобщена Скорость, обобщенные координаты и время. Если обобщенные координаты, такие как qjy, не включены в формулу функции Лагранжа, dLldqs = Q. (42) Обобщенные координаты, которые удовлетворяют условию (42), называются патрулями. Для циклических обобщенных координат qj уравнение Лагранжа принимает вид Тогда получите циклический интеграл уравнения Лагранжа. dlldq ^ Cj, (43) Где С является константой.
Циклические интегралы могут включать производные по времени от обобщенных координат, включая производные по времени, меньшие или равные циклическим координатам 1-го порядка. Таким образом, (43) является, вообще говоря, дифференциальным уравнением первого порядка или обычным, в отличие от уравнения Лагранжа. Если все обобщенные координаты периодические, система уравнений Лагранжа второго порядка заменяется только циклическим интегралом первого порядка. Интегрировать систему линейных уравнений гораздо проще, чем квадратичную систему.
Так как в уравнении с частными производными эти переменные независимы, то последнее уравнение может быть удовлетворено лишь в том случае, если каждая скобка в отдельности равна постоянной. Людмила Фирмаль
Важно найти периодические обобщенные координаты. Используя циклическое интегрирование, так называемый метод игнорирования может уменьшить число уравнений Лагранжа на число периодических координат без увеличения порядка полученного дифференциального уравнения. Другим направлением анализа динамики является поиск интегральной системы самих лагранжевых уравнений или эквивалентной системы. После Лагранжа аналитическая механика получила широкое развитие и применение в различных областях науки и техники. Метод особенно широко используется в теории системной вибрации и квантовой механике. Пример.
Гомогенный диск А с гравитацией Р = 100 Н наматывается на блок В и оборачивается нерастяжимой нитью, прикрепленной к грузу I) с гравитацией f * 2 = 200 Н (рис. 103). , Load O может скользить Зак, что не двигается. Грудная плоскость с углом наклона а = 30. коэффициент Трение скольжения между нагрузкой и плоскостью / = 0,3. Блок Б. Гравитация Р, = 400 Н, принимаем за однородную Если резьба nc скользит вдоль блока, определите как блок c, так и массовое давление, ускорение нагрузки /) и ось диска A, а также натяжение нити блока> cc Трение вала винта игнорируется.
Движение начинается с состояния покоя. L •. К я Решения. Мобильная система имеет две степени свободы. Обобщенные координаты системы берут 5 перемещений произведения по «плоскости и углу». Наклонная нагрузка Кинетическая энергия системы Инерция диска Где vc — центральная скорость Промах! G — радиус диска относительно оси, проходящей через центр диска Блок В вращается вокруг неподвижного Где <р! Является ли угловая скорость блока. Jc g = ось вращения; g} — радиус блока. Груз D) Движение доступа Перпендикулярно плоскости Относительный момент инерции Энергетическая энергия Предположим, что неразвернутая резьба блока ориентирована в положительной плоскости, поскольку она связана со скоростью 1 точка.
- Так что в начале загрузки, ускорение нагрузки вниз. Все вязать Скорость число | s |. Следовательно, такая скорость и точка диска М. Возьмите его с помощью шеста и определите скорость точки по формуле, которая соединяет скорость двух точек тела с плоскостью Где 1> см = L / C | φ |. Когда диск вращается против часовой стрелки, скорость «см» будет вертикально вниз, а когда груз будет перемещен, он будет вертикально вверх I) вниз я — гф, направление вверх f) 2 _ RNf ^ Наклонная поверхность. Следовательно, «с = Выразите кинетическую энергию системы с обобщенной скоростью 2 2 2e 2.
Вычислить производную, которая попадает в левую часть уравнения Лангранжа: д ват зрг д (5тп При расчете обобщенной ss степени тяжести P, Plt P2 И сила трения F наклонной поверхности. Соединение (резьба, вал Нет необходимости рассматривать блоки, гладкие наклонные поверхности). Важно правильно выбрать направление силы трения F. Сила трения F всегда направлена на скорость s перемещения груза D, которая не всегда известна заранее. Предположим, что движение груза происходит вниз, но на наклонной поверхности. Тогда сила трения в противоположном направлении. Решите проблему в этом предположении.
Пластинка 2, расположенная в неподвижной горизонтальной плоскости, шарнирно связана в точке С с круговым диском лежащим в той же плоскости и движущимся вокруг своего неподвижного центра О. Людмила Фирмаль
Если вы используете знак плюс, чтобы получить s (в данном случае s, потому что он начинается из состояния покоя), принятое предположение верно. Если ускорение z (и, следовательно, скорость z) отрицательно, было обнаружено, что ожидаемое направление силы трения направлено вдоль движения нагрузки, поэтому направление силы должно быть обращено вспять, и проблема будет решена снова. Это неправильно Когда j ’= 0, нагрузка не может быть перемещена из стационарного состояния. Как только предполагаемое направление силы трения на наклонной поверхности установлено, вычисляется обобщенная сила Q. В то же время он информирует систему о возможных перемещениях, допускаемых соединением, и под этим углом сообщает движениям, что груз может упасть на рампу 6 секунд.
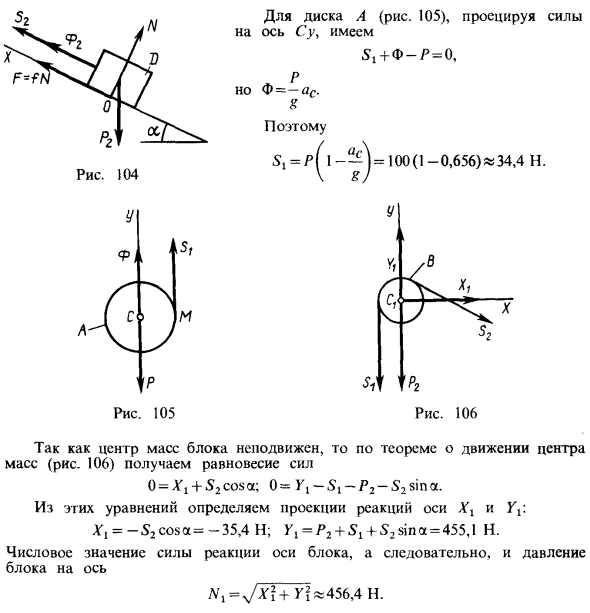
Если φ = const, смещение точки C диска такое же, как смещение точки M, поэтому F = Fmtl = / N сила Pt применяется к неподвижной точке и возможна потому, что возможное движение неподвижной точки равно нулю Вся основная работа по переезду равна нулю. Вертикальная сила реакции на наклонной поверхности определяется из баланса силы нагрузки D в направлении, перпендикулярном наклонной поверхности. У нас есть Имея это в виду b, = Pr (sin <x-f cosa) —P. При расчете обобщенной силы 1 смещение, где изменяется величина 8 <p, и обобщенные координаты положительный В этом случае точка диска М является оростом, 8cc = r8 <p и 8cc положительный 8 <p направление R Другие рабочие места перемещения равны нулю, потому что их очки Go.
Вот так. Одновременные уравнения Уравнение Лагранжа, получить — / cosa) —P; Выразите от φ до s из последнего уравнения. ψ = — (+ + 3). Подстановка этого значения в первое выражение приводит к + .P2j = P2 (sina-7cosa) — ^ Знак плюс для s (в данном случае для s) указывает на то, что, как и ожидалось, движение I) фактически направлено вниз вдоль склона. Ускорение в точке C можно получить путем дифференцирования по времени уравнения скорости Vc = s-rf. Это действует в любое время. У нас есть Вот так. ac = ‘»c = i-r <P = j- ^ (g + i) =» j «= -0,656x = -6,43 м / с2.
Знак минус для переменного тока указывает, что ускорение переменного тока направлено вниз. Это потому, что направление вверх является положительным направлением. Чтобы определить натяжение нити, принцип Дарренвале применяется к нагрузке и диску. Для нагрузки D (рис. 104), которая проецирует силу на ось Ox, получается S2 + <K2-P2sina + / W = 0. но так Н.
Смотрите также:
Задачи по теоретической механике
| Структура уравнений Лагранжа и их составление | Канонические уравнения |
| Уравнения Лагранжа для потенциальных сил | Устойчивость положения равновесия |

