Уравнением с одной переменной называется равенство, содержащее только эту переменную, ее называют неизвестной величиной. Значения переменной, при подстановке которых в уравнение получается тождество, называются корнями уравнения, или решениями уравнения. Решить уравнение — это значит найти все его корни и только их, или доказать, что корней нет. Два уравнения, имеющие одни и те же корни и не имеющие других корней, называются равносильными. Обычно при решении уравнений производят преобразования выражений, входящих в уравнения. Чтобы такие преобразования были равносильными, т.е. не меняли набора корней, необходимо, чтобы корни не терялись и не приобретались посторонние корни. Для этого на каждом этапе преобразования нужно выписывать ограничения на производимые операции. Например, нельзя безоговорочно делить на выражение, содержащее переменную, т. к. это выражение может оказаться нулевым. Нельзя возводить выражение, содержащее переменную, в четную степень, т. к. приобретаются лишние корни.
Мы будем решать различные уравнения, но начнем с рациональных уравнений, т.е. таких, в которых правая и левая части являются многочленами, их произведениями и отношениями. Самые простые из них — линейные уравнения. Это уравнения вида 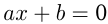 , где
, где 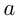 и
и 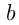 — некоторые постоянные величины и
— некоторые постоянные величины и  . Единственный корень линейного уравнения
. Единственный корень линейного уравнения 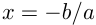 . Например, решим уравнения.
. Например, решим уравнения.
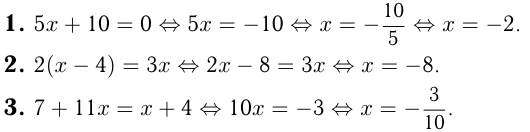
Уравнение вида 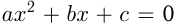 , где
, где 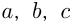 — некоторые числа,
— некоторые числа,  ,
, 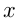 — переменная, называется квадратным уравнением. Корни квадратного уравнения вычисляются по формуле
— переменная, называется квадратным уравнением. Корни квадратного уравнения вычисляются по формуле 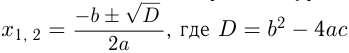 — дискриминант. Если
— дискриминант. Если 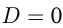 ,то квадратное уравнение имеет один корень
,то квадратное уравнение имеет один корень 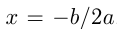 . Если
. Если 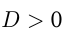 , то квадратное уравнение имеет два корня:
, то квадратное уравнение имеет два корня: 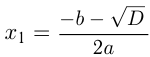 и
и 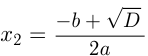 . Если
. Если 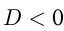 , то квадратное уравнение не имеет корней. Если
, то квадратное уравнение не имеет корней. Если 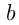 — четное число, т.е.
— четное число, т.е. 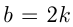 , то корни можно вычислять по формуле
, то корни можно вычислять по формуле  . Если квадратное уравнение имеет вид
. Если квадратное уравнение имеет вид 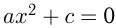 , его корни вычисляются по формуле:
, его корни вычисляются по формуле: 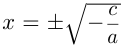 , и они существуют, если
, и они существуют, если 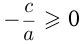 . Если квадратное уравнение имеет вид
. Если квадратное уравнение имеет вид 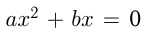 , его корни равны
, его корни равны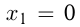 и
и 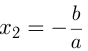 , т. к.
, т. к. 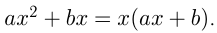
Квадратные уравнения вида  и
и 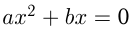 называются неполными квадратными уравнениями.
называются неполными квадратными уравнениями.
Например, решим уравнения:
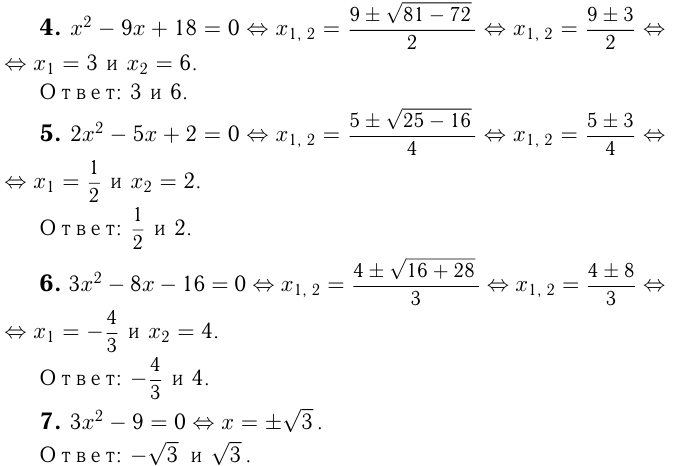
Этот материал взят со страницы решения задач по математике:
Возможно вам будут полезны эти страницы:
| Основные тригонометрические формулы |
| Вычисление значений тригонометрических выражений задачи с решением |
| Квадратные уравнения задачи с решением |
| Биквадратные уравнение задачи с решением |
