Оглавление:





Чистый изгиб. определение нормальных напряжений
- Чистый изгиб. Определение нормы Напряжение Как уже говорилось выше, в сечении балки в момент изгиба возникает изгибающий момент и поперечная сила. При исследовании напряженного состояния удобнее начинать с особого случая, когда боковая сила равна нулю. Таким образом, в центральной части балки, показанной на рисунке. 203, чей собственный вес игнорируется, имеет чистый
изгиб:момент по длине этого участка не изменяет своей величины, и нет никакой боковой силы. Изучите закон распределения напряжений в поперечном сечении балки при чистом изгибе и сможете найти максимальное напряжение. Сначала рассмотрим балку, имеющую поперечное сечение по крайней мере с одной осью симметрии, совпадающей с силовой плоскостью.
Таким образом, одна из инерционных осей находится на плоскости изгиба, а другая Людмила Фирмаль
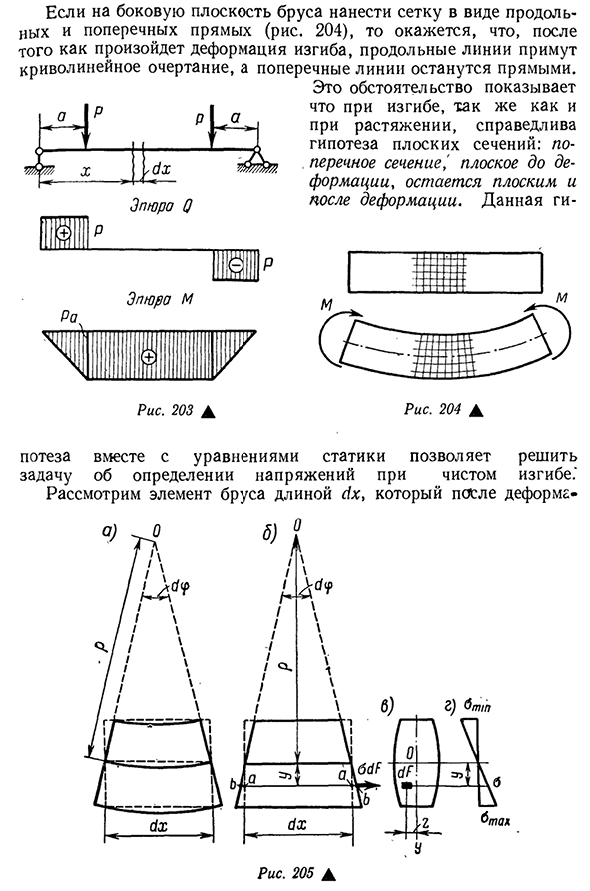
перпендикулярна ей. Для решения этой задачи необходимо привлечь условие деформации в дополнение к статическому условию, которое может быть сформулировано только на основе экспериментального наблюдения. На стороны балки 224if наносят сетку в виде продольных и поперечных линий(рис. После того, как деформация изгиба произошла, обнаруживается, что продольная линия принимает криволинейную форму, а поперечная линия становится
прямой. Участок 0 Участок М Это обстоятельство указывает на то, что при изгибе и растяжении гипотеза о плоском поперечном сечении справедлива. Это ги Рис 204А Эта гипотеза вместе с уравнениями статики позволяет решить задачу определения напряжений при чистом изгибе.’ Рассмотрим элементы балки длиной DX после деформации- 225) — кривая фиг. 205, а). Две смежные секции наклонены, образуя угол между ними. В этих условиях верхние волокна сжимаются, а нижние растягиваются. Волокна, которые
- лежат на определенной высоте, остаются неповрежденными, мы называем их нейтральными. О площади поперечного сечения(рис. 205, в) поверхность, на которой присутствуют нейтральные волокна, образует след нейтрального Луча Oh. Радиус кривизны нейтрального волокна равен оси o, где сечение rotates.It обозначается продольными волокнами и деформируется таким же образом. Для удобства рассуждения на рисунке. 205, б, волокна получают условное изображение деформированных элементов, остающихся на прямой линии. Верхние волокна сжимались, а нижние растягивались.
Согласно этой фигуре, относительное удлинение волокна АА на расстоянии от нейтрального слоя легко установить, что каждый состоит из двух сегментов АИ, равных значению y, следовательно, суммарному удлинению любого волокна. Это будет ДГ/ч-Уду. Но так как YH-rblr, относительное удлинение этого волокна М Х1 Если предположить, что отдельные волокна не прижимаются друг к другу, то каждое из них подпадает под условие простого растяжения (или сжатия). В этом случае для перехода от расширения g к напряжению
o можно использовать простую крюковую зависимость. а=ее= — у.(8.8) П’ Во-первых, мы устанавливаем положение нейтральной линии, Людмила Фирмаль
которая измеряет расстояние y. для этого мы используем тот факт, что результат основной нормальной силы Ayr (т. е. нормальной силы) в поперечном сечении при чистом изгибе равен нулю: Н=] * Эр=0, Г Или I Ом V = 0. Х Р тт Е Но так как умножение-не ноль, но в то же время оно может быть П 2 26винести для знака интеграла(поскольку он не зависит от интегральной переменной), а затем уменьшить его UIR=0. Е Полученный Интеграл представляет собой статический момент площади поперечного сечения относительно нейтральной оси выхлопного газа и равен нулю только тогда, когда ось проходит через центроид сечения. Исходя из этого, можно сказать, что нейтральная ось чистого, прямого изгиба стержня проходит через центр тяжести сечения. Рассмотрим моменты внутренних сил относительно
нейтральной оси. Для этого вычислите сумму моментов основной внутренней силы<z (1P) для этой оси и уравняйте ее с изгибающими моментами: Мг=(ОС?7) У. Е Если вместо напряжения o подставить его значение по формуле (8.8)、 Интегралом, входящим в это уравнение, является момент инерции поперечного сечения стержня) HRM= п Так… Где найти кривизну нейтрального слоя: — (8.9) П Подставляя это выражение в выражение(8.8), можно, наконец, (8.10)) Формула(8.10) позволяет определить напряжение в любой точке горизонтальной линии поперечного сечения пучка, удаленной от нейтральной оси на расстояние Y. график, Закон изменения напряжений на высоте 227 интервала называется диаграммой напряжений. Для риса. 205 g
показывает график давления при чистом изгибе. Самое высокое напряжение-это точка, в которой значение y принимает наибольшее значение, то есть самое дальнее волокно. При выводе формулы (8.10) мы предположили, что поперечное сечение стержня симметрично относительно оси Oh. Однако это предположение было сделано только для удобства рассуждений. Получается, что формула (8.10) может быть использована для любого поперечного сечения, но при этом предполагается, что одна из главных осей инерции находится в плоскости нагрузки. Чтобы доказать последнее утверждение, мы приравниваем к нулю момент инерции всех основных внутренних
сил относительно оси OU. Это следует UGR=0. п Поскольку известно, что это значение равно центробежному моменту инерции сечения, ось Y и ось g являются главными осями. Для симметричного поперечного сечения, учитываемого при выводе, оси y и d являются главными центральными осями. Для других поперечных сечений плоскость груза должна быть параллельна центральной оси.
Смотрите также:

