Оглавление:







Чистый изгиб
Чистокровный. В предыдущей главе мы упоминали, что величина напряжения на любом поперечном сечении балки определяется боковой силой этой детали и величиной изгибающего момента. При приложении боковых сил напряжение определяется с самого начала. Равный нулю, есть только изгиб moment. In этот случай, он называется Чистым bend. An пример такого изгиба показан на рисунке. 81.
- Из условий Сима метрический. мы Реакция в этом случае; и я Р. Р. считать равным — \ p ^ p По новой части балки на левой стороне поперечного сечения mp%можно сделать вывод, что внутренние силы распределены вдоль поперечного сечения. 81.. ’: о. *%ля Поперечное сечение должно быть равно статическому изгибающему моменту Ra и равно паре сил в противоположном направлении, представляющих собой работу отбрасываемой правой части TP и левой beam.
To найдя законы распределения этих внутренних сил по поперечному сечению, необходимо учитывать деформацию beam. In в случае простой балки с симметричной продольной плоскостью с внешней изгибающей парой, действующей в этой плоскости, изгиб происходит в той же плоскости.
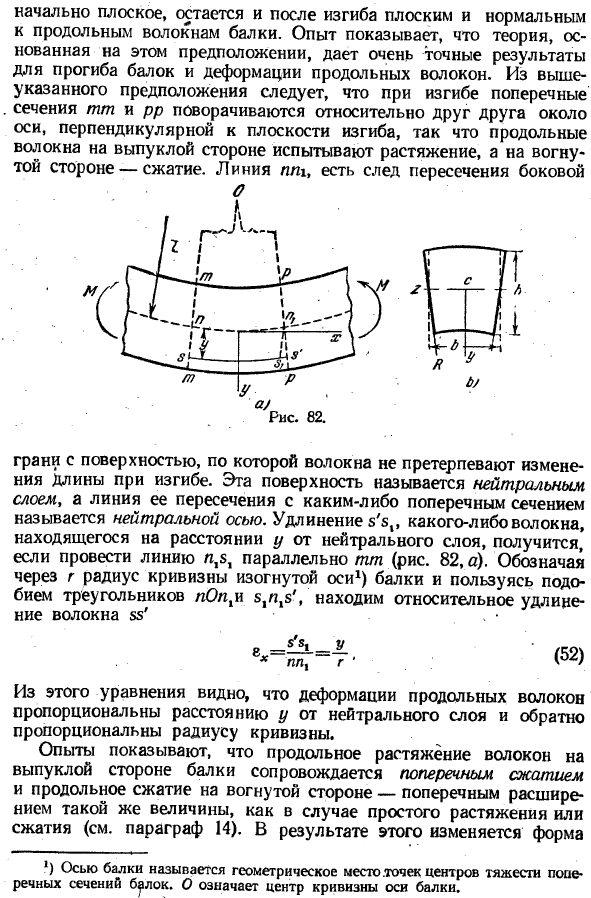
Если поперечное сечение балки прямоугольное, а на ее поверхности нанесены 2 смежные вертикальные линии ТТ и ПП, то видно, что эти линии остаются прямыми при изгибе и вращении, поэтому они остаются перпендикулярными продольным волокнам балки (рис.82)
Теория изгиба, описанная ниже, основана не только на предположении, что линии, проведенные по краям, такие как TT, остаются прямыми, но и на предположении, что все поперечное сечение балки (первоначально плоское) является плоским после изгиба и перпендикулярным продольным волокнам балки. Людмила Фирмаль
Опыт показывает, что теория, основанная на этом предположении, дает очень точные результаты для отклонения луча и продольной деформации волокна. Из приведенного выше предположения следует, что при изгибе поперечные сечения ТТ и ПП вращаются относительно друг друга вокруг оси, перпендикулярной плоскости изгиба, так что выпуклые продольные волокна подвергаются растяжению и сжатию в вогнутой стороне.
Линия PPG, есть следы пересечения сторон Да. К Да. Рисунок 82. Края поверхности, где волокна не изменяются. Эта поверхность Называется нейтральным слоем, а пересечение с любым поперечным сечением называется нейтральной осью. Удлинение B’b4 волокон на расстоянии y от нейтрального слоя получается, если линию l, b провести параллельно линии TT(рис. 82, а).Обозначим радиус кривизны изогнутой оси пучка через r и воспользуемся подобием треугольника nOphi b ^ b ’, чтобы найти относительное удлинение волокна BB’.
Из этого уравнения видно, что деформация продольных волокон пропорциональна расстоянию y от нейтрального слоя и обратно пропорциональна радиусу кривизны. Эксперимент показывает, что продольное растяжение волокон на выпуклой стороне пучка сопровождается боковым сжатием, а продольное сжатие на вогнутой стороне сопровождается боковым расширением той же величины, что и в случае простого растяжения или сжатия(см. п. 14). * ) Ось луча является локусом точки центра тяжести сечения b ^ lok. O означает центр кривизны оси балки.
В поперечном сечении, как показано на фиг. 82 b, вертикальные стороны прямоугольного поперечного сечения наклонены друг к другу. Относительная деформация в поперечном направлении (53) Где IX-коэффициент Пуассона. Это искажение приводит к тому, что все линии в поперечном сечении, параллельные оси z, изгибаются так, что они перпендикулярны стороне поперечного сечения.
Радиус кривизны/?Только в несколько раз больше, чем r из ex, который численно больше, чем e (см. уравнение 53)、 I = 1 г (54) Из продольной деформации волокна соответствующее напряжение определяется на основе закона крюка (уравнение 4). 0,= ^ * Г (55) Законы распределения этих напряжений показаны на рисунке. 83.
Напряжение волокна пропорционально расстоянию от нейтральной оси расположение нейтральной оси и радиус кривизны r (2 неизвестных в уравнении (55)) можно определить из условия, что сила, распределенная в поперечном сечении балки, создает пару сопротивлений, уравновешенную внешней парой M (рис.81). 。 Dp означает основную площадь поперечного сечения на расстоянии y от нейтральной оси (Рисунок 83).
Сила, действующая на эту базовую платформу Произведение напряжения на площадь yP (уравнение 55), то есть-yP Все такие силы, распределенные в поперечном сечении, представляют собой систему сил, соответствующих парам сил, так что результат действия этих сил равен нулю и становится:
То есть статический момент площади поперечного сечения относительно нейтральной оси равен zero. As в результате нейтральная ось проходит через центр тяжести секции. Момент усилия на базовом сайте (Относительно нейтральной оси 1р равно ууу. Все итоги Предполагая такой момент вдоль поперечного сечения и синтетический момент, равный моменту м внешней силы, получается следующая формула для определения радиуса кривизны R. Или 1 -^. (56)
Среди них Существует момент инерции поперечного сечения относительно нейтральной оси r (приложение п. (см. 350).Из уравнения (56)видно, что кривизна прямо пропорциональна изгибающему моменту и обратно пропорциональна величине изгибающей жесткости балки. Исключение r из уравнений (55)и (56)дает следующее уравнение для определения напряжения: (57)
В этом уравнении, как показано на Рис. 5, момент M, вызывающий изгибную деформацию за счет выпуклой части, является положительным. 82; координата y положительна вниз. Было приведено предыдущее рассуждение. Для прямоугольных cross-section. It также эффективен для балок с другими формами поперечного сечения.
Максимальные растягивающие и сжимающие напряжения возникают в крайних волокнах. Людмила Фирмаль
- В таких случаях изгиб происходит на рабочей поверхности пары, а поперечное сечение остается плоским и перпендикулярным продольным волокнам даже после изгиба.
Также в прямоугольном или любом месте Другое поперечное сечение с центроидом вдоль серого К середине высоты A относится случай y =±2.Тогда он берется в случае положительного М. Единое время.»Э (ОЖ) m1n =-57—(58) Для простоты используйте следующие обозначения: (5Э) И затем… «Юта,= U. (0) w1n = * — (60)
Величина V / g называется моментом сопротивления площади поперечного сеченияния. Для прямоугольного сечения(рис. 82, б)мы имеем. В’ • • * ТГ ’ Для круглого поперечного сечения с диаметром<1、 Т yaa4t-паа) л-автомат АГ ’■■; — Заводские значения Jt и\РЯ перечислены в справочной таблице для различных фактически используемых профилей, таких как двутавровые балки и каналы.
В приложении представлена таблица таких разделов. Если центроид поперечного сечения находится не в середине высоты, например, для Т-образной балки, а для S И-La означает расстояние от нейтральной оси, соответственно Волокна нижнего и верхнего полюсов, а также положительные изгибающие моменты, дают»». <- И-М5* -. (В Из-за отрицательного изгибающего момента、 К) ТХ= -^. (о)»10 = м ^ — (62) * г’.Ж. » ^ г В.
Задачи 1.Определить максимальное напряжение оси Локомотива* «(рис. 84).c= 33,75 см, диаметр вала<1-25 см, нагрузка P, передаваемая на шейку вала пружиной, составляет 10 400 кг. Решение. Изгибающий момент, действующий на центральную часть бухты, будет равен M Pc » 10 400-33. 75 кг.
Согласно формуле (60), максимальное напряжение составляет °<Р7°°-230. 2.Если материал стальной, а расстояние между центрами шейки составляет 147,5 см, то в предыдущей задаче определяют радиус кривизны g и прогиб оси. Решение. Радиус кривизны R, уравнение•(55) — замещенных Р 1 / А■> / В ——— * Y = −12,5 см, (a) Шах » 230 кг / СМГ. Тогда n £6 2-10M2. 5, почтовое отделение № — а.’2〜= 250’〜 = 108700 см. Рис.84.
Обратите внимание, что при вычислении /(рис. 84) ось кривой представляет собой дугу Окружность радиусов r и yB представляет собой прямоугольный треугольник вокруг ноги. Где o-центр окружности. Так… Вт — р * — (р-р?= Ч1-Т-、 /Очень мало по сравнению с радиусом r, и в этом уравнении мы используем значение/ * Двухместный 147.5 * 2р 8 * 108,700 Ф= −0,025 см.
3.Деревянная балка с квадратным поперечным сечением 25×25 см опирается на A и B (рис.84), и на обоих концах приложена сила P. Для AB = 180 см, s = 30 см, (stL) goax = 67 кг / см *и E = \ 0 * кг / см определите величину P и Центрального прогиба. Вес балки игнорируется. Построить график боковых сил и изгибающих моментов. Ответ. P = 5816 кг,/ = 0,217 см. 4.As как показано на рисунке, поддерживаются двутавровые балки высотой 75 см.
Он нагружается на консоль с равномерно распределенными нагрузками 85 и 13 300 кг / м. Для 1K = 357 400 см определите максимальное напряжение в центре балки и отклонение в центре балки. SH II11 。 6.0 м►< — L0m -± Shchsm \ суфиксом z — См. Рисунок 85. Решение. Изгибающий момент в центральной части балки равен/И=13300-ЗХX150 = 5 985 000 кгсм. ’ , в М 5 985 000-37. 5 СУ. нет. (^x) Макс ^ 7 357 400 * число{см, f-0,377 см.
5.При намотке на круглый барабан диаметром D = 50 см определяют максимальное напряжение, возникающее на стальной проволоке диаметром a = 0,08 см. Решение. Максимальное удлинение от изгиба по формуле (52)составляет 。 д 0.08 Е Д + Д-50 Соответствующее растягивающее напряжение равно stx)ha «= £е= −10’50°’08-= 3200 кг / см .
6.Стальная линейка с поперечным сечением 0. 08×5 и длиной f = 25 см изгибается парой сил, приложенных к обоим концам по дуге 60°.Определите максимальное напряжение и прогиб. Решение. Радиус кривизны r равен формуле g » = 23,9 см, а максимальное напряжение по формуле (55) « * ) Макс= = 3350 кг! См. \ Отклонение, рассчитанное для дуги окружности, равно f = r(1-cos 30°)= 3,2 см
7.Если максимальный прогиб в центре равен 2,5 см, то в предыдущем выпуске определите величину максимального напряжения и силы, приложенной к обоим концам линейки. Ответ. (0L) Ш4Х= 2560 кг / с. i*, м-6,83 kgcm.8.By нагревая неравномерно по высоте L поперечного сечения, определим кривизну, возникающую в свободно лежащей стальной балке прямоугольного сечения.
Температура любой точки на расстоянии y от центральной плоскости пучка xg (рис. 82) равна, С- ’ О) У 2 л Где температура в нижней части балки,/ in-температура в верхней части,/, — / 0 = 70°C, а коэффициент линейного расширения равен ac = 125 * 10 » 7.Что происходит с напряжением, когда оба конца балки герметизированы?
Решение. Температура xr в центральной плоскости постоянна, -> 0-и измеряет следующее: Изменение температуры другого волокна пропорционально. Соответствующее относительное удлинение и укорочение температуры также пропорционально y. то есть оно следует тем же законам, что и деформация, определенная в Формуле(52).
Результатом неравномерного расширения этого волокна будет изгиб балки, а радиус кривизны r можно определить по формуле (52). * А-(Л -/») ’ * * — Г ———Это будет-и-ы вместо-ы. а потом… 1143 собой. <М./- |<) Если оба конца балки герметизированы, то прекращение вызовет пару реактивных сил такой величины, что разрушит кривизну от неоднородного нагрева в месте прекращения. Отсюда г 1143 л ’
Если мы присвоим его формуле (57)、 ’•г — ЕС * 1143/1 И максимальное напряжение тока £ (^x) проверка = 2 ″ 1143 кг / см *. 9.Если дуга соответствует 10°и материалом является медь, то мы решим задачи b и 7. 10.Решаем задачу 4, предполагая, что балка деревянная, поперечное сечение составляет ZOX gO см, а сила распределенной нагрузки равна 1300 кг / м. рассчитываем изгибающий момент и силу сдвига.
Смотрите также:
Предмет сопротивление материалов: сопромат

