Оглавление:


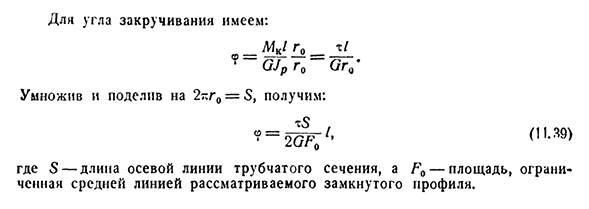

Чистое кручение стержней некруглого сечения
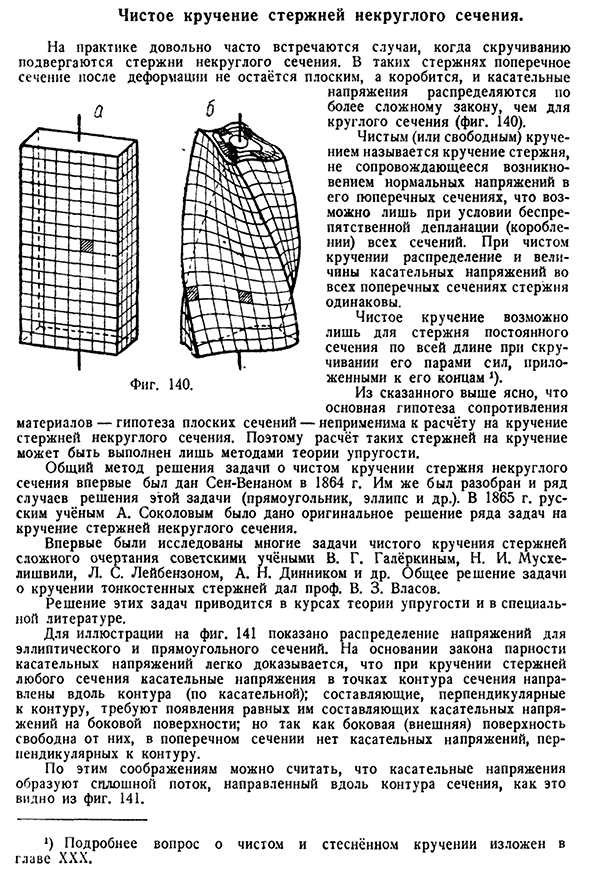
- Чистое кручение стержня в некруглом сечении. На практике встречается довольно много случаев, когда стержень некруглого сечения подвергается скручиванию. В таком стержне поперечное сечение после деформации не плоское, а искривленное, и тангенциальное напряжение распределяется по более сложному
закону, чем в круговом сечении(рис. 140). Чистая (или свободная) закрутка-это закручивание стержня без возникновения нормальных напряжений в его поперечном сечении, при условии неупорядоченности (искривления) всех сечений при чистой закрутке распределение напряжений сдвига и величина всех поперечных сечений стержня одинаковы. Чистое кручение возможно только
для стержня определенного поперечного сечения по всей длине, при Людмила Фирмаль
скручивании его с помощью пары сил, приложенных к его концам.*). * ) Для получения дополнительной информации о чистых и сдержанных поворотах см. главу XXX. Из вышесказанного ясно, что основная гипотеза сопротивления материала (гипотеза плоского сечения) неприменима к расчету торсионных стержней некруглого сечения. Поэтому расчет такого стержня на кручение может быть
осуществлен только методом теории упругости. Популярный метод решения задачи чистого скручивания стержня некруглого сечения был впервые предложен Сен-Венаном в 1864 году. Он также проанализировал множество случаев решения этой задачи (прямоугольники, овалы и др.).да что с тобой такое? В 1865 году русским ученым А. Соколовым было дано собственное решение многих задач с закрученными стержнями некруглого сечения.
- Многие проблемы с чистым скручиванием палки сложной формы советский ученый В. Г. Галеркин, Н. И. Муще-лишвили, л. с. Лейбензон, A. N. It был впервые исследован Динником и другими. Общее решение задачи скручивания тонкостенных стержней дано профессором В. Брашов Решение этих задач дается в курсах теории упругости и специальной литературы. О примере на рисунке. 141 показано распределение давления для эллиптического и прямоугольного сечений. Исходя из закона касательных напряжений пары, видно, что торсионный стержень любого касательного напряжения в точке сечения контура направлен вдоль контура (в тангенциальном направлении). По этим причинам можно предположить, что тангенциальное напряжение образует
непрерывный поток, направленный вдоль контура сечения, как показано на рисунке. 141§ 67]некруглое сечение 213 полюс кручения Таблица все для агрегатов теории упругости, полученных по некоторым результатам Лицо 17. При необходимости. Вместо этого вводят значение полярного момента инерции Jp 4, также выраженное в единицах длины четвертой степени и зависящее от размера сечения, вместо Wp-Wp и тех же этих геометрических характеристик’и’. Таблица 17 демонстрирует новый вид, самый большой из витых рогов T / PIA Фигура. Сто сорок один / 77(7* Г ♦ т. Но Сечение условно называют моментом инерции при
кручении 4 сопротивления кручения U7K. Некоторые формы поперечного Людмила Фирмаль
сечения(круги, кольца) 4=4,wк = WР. Чтобы использовать таблицу 17, у вас есть следующая формула:: A1K Т Шах — ^к»(11.34) (11.35 утра) Для этого, если происходит скручивание стержня сложного сечения, который можно разделить на части тонкостенными элементами.: 4-Ли 4 ″ Lez4 — * * * — Б Где N=1,2,3,. — Количество тех основных частей, на которые делятся секции. Потому что угол скручивания для всего сечения и всех деталей одинаков: е _A1KZ _ — ATKiZ_A4KnZ v GJK~G J Ki~» — G J K n’ Крутящий момент распределяется между отдельными частями секции пропорционально ее жесткости: Таким образом, максимальное касательное напряжение в каждой части (h) сечения составляет、: Т а б л и Ц А17 д
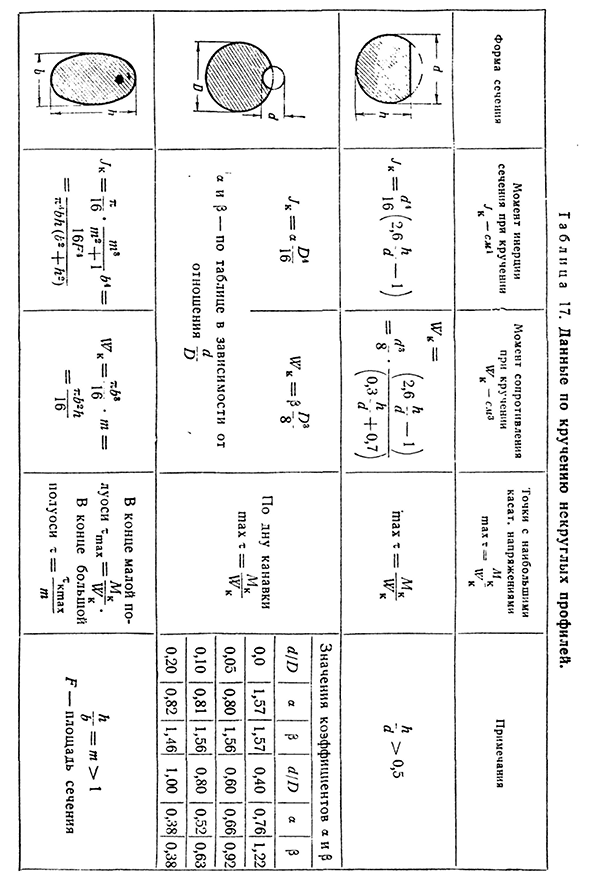
н ы е по К Р У Ен и Й Н Е К Р У ГЛ ы х П РОФ и лей. Точка с наибольшей касательной. Напряжение тока максимальное т=а «„К Замечания Момент сопротивления в повороте XV-p “ z» К Момент инерции сечения при кручении< / K_SML Знак ч д 0,5 К^ Макс Т — Знак согласно таблице согласно коэффициенту A и p-d Д ф В нижней части паза Значения коэффициентов a и p d/D A dJD a≥ О, О1,57 1,57 0,40 0,76 1,22 0,05 0,80 1,56 0,60 0,66 0,92 0.10, 0.81, 1.56, 0.80, 0.52, 0.63 0.20 0.82 1.46 1.00 0.38 0.38 214 проверка прочности на кручение С б… я Тонны / Р2+1 16L4 Uosi t tah в конце малой по-l4k= — ^ — t в конце большой полуоси Т-ctah Тонны х. г= » >1 F-поперечное сечение ■ б» Hjp
не р О Д О Л Ж Е Н И Е таб л. Семнадцать. Форма поперечного сечения Крутящий момент инерции секции Момент сопротивления кручению W-cm * K Точка с наибольшей касательной. Напряжение X T = = 1^K Замечания X в конце небольшой по-посещая Гуйлинь-го = ^-т в конце Х большой полуоси== = ^^ — г- — — г — =т>1, Би Б2 ^2__^2___1 — Т■—<Х1 • Хи-БТ с низкой толщиной & может сделать даже распределение поперечного сечения: Равномерное распределение напряжения Тонны М К 2л& L = UZK= В середине длинной стороны L4C Тахт-Т=7Т Шах в середине короткой стороны * угол натяжения-равен нулю Мама В НПР Значения коэффициентов а, р и 7 приведены
в таблице. II Но Семь. 1,0, 140, 0,208, 1-0. 1.5 0.294 0.346 0.859 2,0 0,457 0,493 0,795 3,0 0,790 0,801 0,753 4,0 1,123 1,150 0,745 § 6 7] кручение стержня некруглого сечения 2 1 5П Р О Д О Л Е Н И Е Т АБ л. Семнадцать. Форма поперечного сечения Момент инерции кручения 4 секции-СМГ Кручение wvk момент сопротивления-см. Точка с наибольшей касательной. Напряжение Макс. г — * 4= ) 3^К=(т-0.63) с z>3 (до-0.63 3 С точки зрения длинной стороны, за исключением углов. Знак m A x T=vrK — В середине короткой стороны, напряжения тока равны Т=0>7 4Г тах Замечания т=ч / Б3 7 6,0 1,789 1,789 0,743 8,0
2,456 2,456 0,742 10.0, 3,123, 3,123, 0,123 Для T= — >4 можно использовать обе таблицы коэффициентов a, p и(Формула приведена здесь 2l/^6л _ _ лозы+ВХ-ОЖ-65 WK1=2 / godb \ГКЗ=2=2 В середине длинной стороны Т1==Ш^ Уз В середине короткой стороны М К Микрограммы Во внутренних углах наблюдается высокая концентрация давления, которая достигает предела текучести материала. При наличии радиуса округления g допускается коэффициент концентрации ^2 216 поворотов. Испытание на прочность [глава XI§ 67]некруглое кручение стержня 217 Наибольшее значение t, которое достигает
этого элемента, будет максимальным значением. Затем v и J CP Шах л кВт ’ т / Макс-U и V Куда? И — ^К Р ] №. КИИ / тах В дополнение к таблице 17 мы приводим формулу и t для сечений, состоящих из узких и длинных прямоугольников, таких как: угловые, Т-образные, двутавровые балки, ванны и т. д. В этом деле、 =Л4″, Где B-короткая сторона, а H-длинная сторона прямоугольника, которая позволяет разделить разделы. Коэффициент V) зависит от формы сечения、: (11.36)) Для этого Для угловой секции……….. vj=1.00, > I луч>y=1.20,>t
луч»……….. =1.15, > корыто>g,=1.12. Угол<Р выражается с помощью выражения Максимальное касательное напряжение можно ожидать в самой широкой части прямоугольника, разделяющего профиль. Это напряжение можно рассчитать по формуле Т Шах ^К^тах4′ (11.37)) wheres&t Ah-это наибольшая толщина среди всех толщин рисунка. Для расчета кручения трубчатых стержней некруглого сечения с малой толщиной стенки используют формулу, полученную в круглом круговом сечении. Момент сопротивления кольцевой части тонкой стенки в соответствии с формулой (11.16) равен:^=2zrt=2F0r
, где Fo-площадь окружности, ограниченная средней линией кольца, t-его толщина. Предполагая, что касательное напряжение равномерно распределено по поперечному сечению кольца: =(П. тридцать восемь) Эта формула может быть использована для расчета некруглого замкнутого сечения тонкостенных стержней.218 кручение, испытание на прочность[глава XI Для угла скручивания мы имеем: _mkz’o’ gjp g o GrQ2T умножаем и делим на: G0=8, получаем: 4-2G F t1, (11.39) где S-длина оси трубчатого поперечного сечения, Fo-площадь, ограниченная средней линией рассматриваемого замкнутого контура.
Смотрите также:
| Внешние и внутренние силы | Общие понятия о деформации изгиба.Устройство опор балок |
| Напряжения. Метод сечений | Характер напряжений в балке. Изгибающий момент и поперечная сила |

