Числовые равенства и неравенства
Обратимся к геометрической интерпретации действительных чисел на числовой прямой. Введём понятие числовой прямой. Пусть на плоскости дана некоторая прямая (обычно расположенная горизонтально). Зафиксируем на этой прямой точку О и назовём её началом отсчёта. Точка О разбивает прямую на два луча. Направление вдоль прямой направо от точки О назовём положительным направлением, а противоположное направление — отрицательным. Пусть также задан отрезок, длина которого принята за единицу длины. В таких случаях говорят, что на прямой введён масштаб.
Прямую, на которой выбрано начало отсчёта, положительное направление и введён масштаб, называют числовой прямой.
Каждой точке числовой прямой можно поставить в соответствие действительное число по следующему правилу:
- Началу отсчёта точке О ставится в соответствие число нуль.
- Каждой точке N на положительном луче ставится в соответствие положительное число а (где а — длина отрезка ON , выраженная через единичный отрезок).
- Каждой точке М на отрицательном луче ставится в соответствие отрицательное число b (где |b|— длина отрезка ОМ , измеренная посредством единичного отрезка).
В результате получим, что при выбранном масштабе:
- каждой точке на числовой прямой поставлено в соответствие одно (и только одно) действительное число;
- разным точкам числовой прямой поставлены в соответствие разные числа;
- нет ни одного действительного числа, которое не соответствовало бы какой-либо точке на числовой прямой.
В таких случаях принято говорить, что между множеством всех точек числовой прямой и множеством всех действительных чисел установлено взаимно однозначное соответствие.
Если на прямой выбрано начало отсчёта, положительное направление и введена масштабная единица, то говорят также, что на прямой задана система координат. При этом сама прямая называется координатной осью, а точка О —началом координат. Действительное число, поставленное каждой точке этой прямой по указанному выше правилу во взаимно однозначное соответствие, называют координатой точки в заданной системе координат.
Рассмотрим теперь два произвольных действительных числа
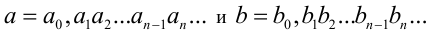
Выше для любых действительных чисел а и b была определена операция сравнения. Применяя сё, получим по отношению к этим числам, что справедливо одно (и только одно) из следующих трёх утверждений:
1) число а равно числу b (а = b); 2) число а больше числа b (а > b)
3) число а меньше числа b (а < b).
В первом случае два равных числа будут обозначаться одной точкой на числовой прямой. Если а > b , то на числовой прямой точка, соответствующая числу а , будет лежать правее точки, соответствую-щей числу b . Наконец, если а < b, то наоборот, точка, соответствую-щая числу а , будет лежать левее точки, соответствующей числу b .
В данном параграфе при сравнении между собой действительных чисел будем пользоваться следующими вполне естественными утверждениями, вытекающими из определений операции сравнения действительных чисел и арифметических операций над действительными числами.
Утв. 1. Два действительных числа а и b равны тогда и только тогда, когда их разность равна нулю, т.е.
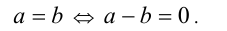
Два действительных числа а и b не равны тогда и только тогда, когда их разность не равна нулю, т.е.
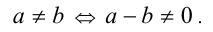
Утв. 2. Число а больше числа b тогда и только тогда, когда разность а —b положительна, т.е.
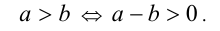
Утв. 3. Число а меньше числа b тогда и только тогда, когда разность а — b отрицательна, т.е.
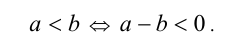
В ситуации, когда число а либо меньше, либо равно числу b (допускается возможность обоих случаев), используется специальное обозначение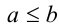 
. Если же число а либо больше, либо равно числу b , используется обозначение 
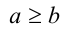. Знаки > (больше), < (меньше),
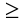(больше либо равно),
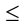(меньше либо равно),
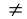(не равно) называют знаками неравенств. При этом знаки > и < относят к строгим знакам, а знак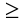и и 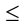— к нестрогим знакам.
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:
