Оглавление:
Числовые равенства и их свойства
Обратимся к наиболее важным свойствам числовых равенств. Но вначале приведём определение числового равенства. Если два числа а и b (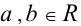 ) соединены знаком равенства а = b , то говорят, что задано числовое равенство.
) соединены знаком равенства а = b , то говорят, что задано числовое равенство.
Пусть a,b ,c,d — произвольные действительные числа. Примем без доказательства следующие свойства. Обратите внимание, что некоторые из них сформулированы в виде достаточных условий, в то время как другие имеют вид необходимых и достаточных условий.
Свойства числовых равенств
- Число а равно числу b тогда и только тогда, когда число b равно числу
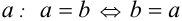 (коммутативность равенств).
(коммутативность равенств). - Если число а равно числу b , а число b при этом равно числуc то число а равно числу c :
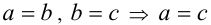 (транзитивность равенств).
(транзитивность равенств). - Если два верных равенства почленно сложить, то в результате также получится верное равенство:
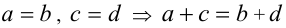 (почленное сложение равенств).
(почленное сложение равенств). - Если два равенства почленно перемножить, то в результате также получится верное равенство:
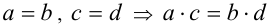 (почленное умножение равенств).
(почленное умножение равенств). - К обеим частям равенства можно прибавлять (вычитать) одно и то же число, в результате также получится верное равенство:
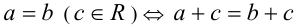 (прибавление числа к равенству).
(прибавление числа к равенству). - Обе части равенства можно умножать (делить) на одно и то же неравное нулю число, в результате также получится верное равенство:
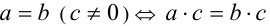 (умножение равенства на число).
(умножение равенства на число). - Обе части равенства (при условии их неотрицательности) можно возводить в произвольную натуральную степень, в результате также получится верное равенство:
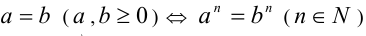 (возведение равенства в натуральную степень).
(возведение равенства в натуральную степень).
Замечание. Последнее свойство, например, вытекает из того, что поскольку 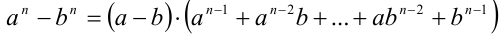 а выражение во вторых скобках не равно нулю (при неравных нулю одновременно а и b ), то разность
а выражение во вторых скобках не равно нулю (при неравных нулю одновременно а и b ), то разность 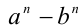 обращается в нуль тогда и только тогда, когда обращается в нуль разность а — b.
обращается в нуль тогда и только тогда, когда обращается в нуль разность а — b.
Пропорции,их свойства
Пропорцией (от латинского ‘proportio’ — соотношение, соразмерность) называют равенство двух отношений:
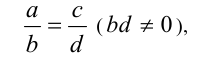
где числа a,b,c,d называются членами пропорции, при этом a и d называют крайними членами пропорции, b и c — средними членами пропорции. Другая форма записи пропорции а : b =c : d . Пропорция, в которой средние члены равны (b = c ), называется непрерывной, и тогда средний член b непрерывной пропорции равен среднему геометрическому (среднему пропорциональному) крайних членов:
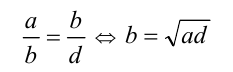
(при условии, что b положителен).
Свойства пропорций
- Основное свойство пропорции: ad = bc (произведение средних членов пропорции равно произведению ее крайних членов).
- В пропорции а/b = c/d можно менять местами средние (а/с= b/d) или крайние члены (d/b = c/а ), или те и другие одновременно (d/c = b/а).
- Если дана пропорция a/b = c/d , то справедливы следующие пропорции (их называют производными пропорции, это следствия из данной пропорции):
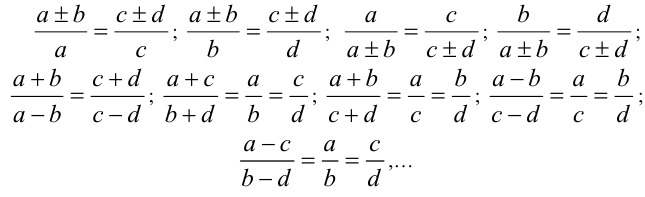
Эти и множество других производных пропорций могут быть объединены в двух основных формах:
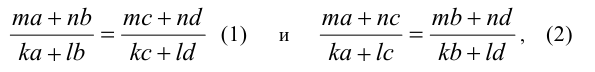
где m,n,k,l — произвольные действительные числа, и знаменатели дробей не обращаются в нуль. Например, при m = n= k = 1 и l = 0 по формуле (1) имеем: (а + b)/а = (с + d)/c. При тех же значениях m,n,k,l по формуле (2) получим: (а + с)/а= (b + d)/b , или, переставляя средние члены пропорции, (а + c)/(b + d)= а/b и так далее.
Если даны несколько равных между собой отношений
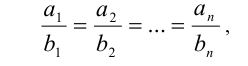
то справедливы равенства
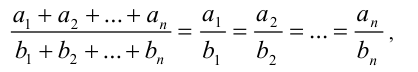
где 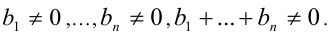
Обобщение свойства 4.
Если 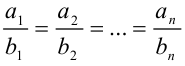 , то
, то 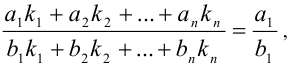
где 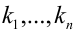 не все равны 0 , причём
не все равны 0 , причём 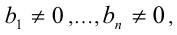
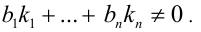
Если 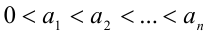 и
и 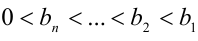 , то верно неравенство
, то верно неравенство
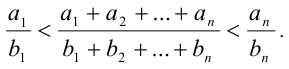
Доказательство. Воспользуемся тем, что среднее арифметическое n различных положительных чисел принимает значение строго между наименьшим и наибольшим из этих чисел:
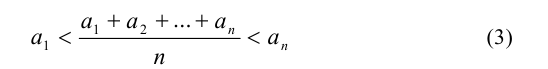
и
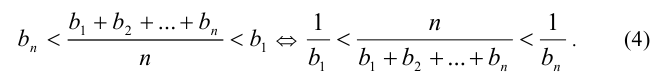
Перемножая неравенства (3) и (4), получаем доказываемое неравенство.
Пример . Пусть 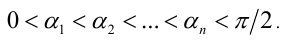 Доказать, что
Доказать, что 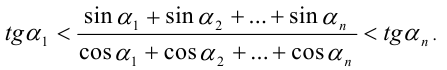
Доказательство. Известно, что если 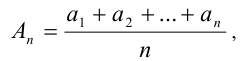 где
где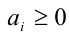
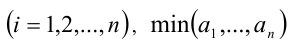 и
и 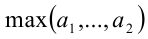 — соответственно наименьшее и наибольшее из чисел
— соответственно наименьшее и наибольшее из чисел 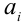 , то
, то
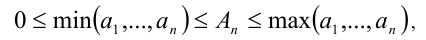
причём среднее арифметическое 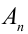 совпадает с наименьшим (наибольшим) из этих чисел тогда и только тогда, когда
совпадает с наименьшим (наибольшим) из этих чисел тогда и только тогда, когда 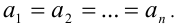 Так как
Так как
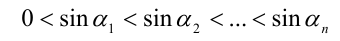
и
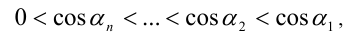
то
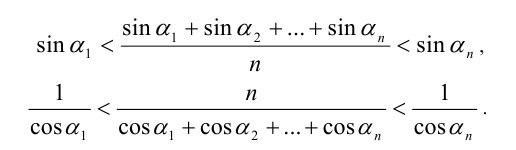
Перемножая эти неравенства, получим окончательно, что
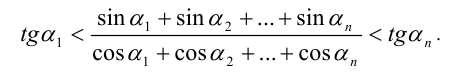
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:

