Оглавление:
Числовая последовательность
Под числовой последовательностью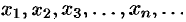 
понимается функция
заданная на множестве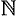 
натуральных чисел. Кратко последовательность обозначается в виде 
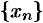или 
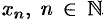. Число 
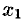называется первым членом (элементом) последовательности, 
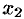— вторым, … , 
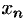— общим или 
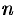-м членом последовательности.
Чаще всего последовательность задается формулой его общего члена. Формула (15.1) позволяет вычислить любой член последовательности по номеру 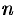, по ней можно сразу вычислить любой член последовательности. Так, равенства
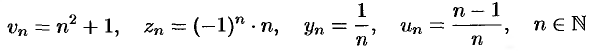
задают соответственно последовательности
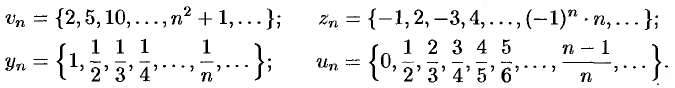
Последовательность 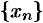называется ограниченной, если существует такое число 
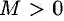, что для любого 
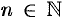выполняется неравенство
В противном случае последовательность называется неограниченной. Легко видеть, что последовательност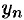и 
и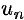 
ограничены, a 
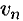и 
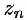— неограничены.
Последовательность 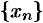называется возрастающей (неубывающей), если для любого 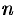выполняется неравенство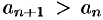 
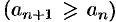. Аналогично определяется убывающая (невозрастающая) последовательность.
Все эти последовательности называются монотонными последовательностями. Последовательности , и 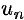монотонные, а 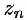— не монотонная.
Если все элементы последовательности 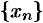равны одному и тому же числу 
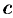, то ее называют постоянной.
Другой способ задания числовых последовательностей — рекуррентный способ. В нем задается начальный элемент 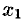(первый член последовательности) и правило определения 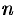-го элемента по ( 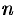— 1)-му:
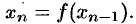
Таким образом,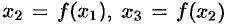 
и т. д. При таком способе задания последовательности для определения 100-го члена надо сначала посчитать все 99 предыдущих.
Предел числовой последовательности
Можно заметить, что члены последовательности 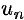неограниченно приближаются к числу 1. В этом случае говорят, что последовательность 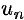, 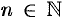стремится к пределу 1.
Число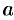 
называется пределом последовательности 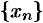, если для любого положительного числа 
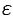найдется такое натуральное число 
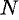, что при всех 
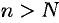выполняется неравенство
В этом случае пишут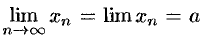 
или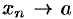 
и говорят, что последовательность 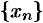(или переменная 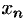, пробегающая последовательность 
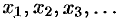) имеет предел, равный числу 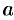(или 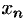стремится к 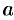). Говорят также, что последовательность 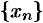сходится к .
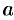Коротко определение предела можно записать так:
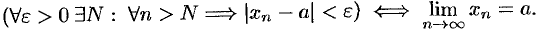
Пример №15.1.
Доказать, что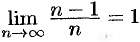 
.
Решение:
По определению, число 1 будет пределом последовательности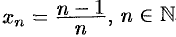 
, если 
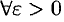найдется натуральное число 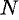, такое, что для всех 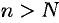выполняется неравенство 
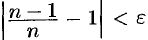, т. е. 
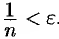Оно справедливо для всех 
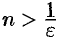, т. е. для всех 
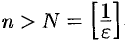, где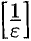 
— целая часть числа 
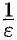(целая часть числа 
, обозначаемая 
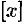, есть наибольшее целое число, не превосходящее ; так [3] = 3, [5,2] = 5).
Если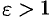 
, то в качестве 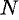можно взять 
.
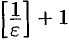Итак, 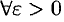указано соответствующее значение 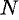. Это и доказывает, что 
.
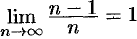Заметим, что число 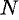зависит от 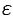. Так, если 
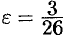, то
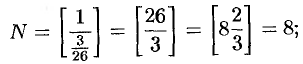
если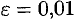 
, то
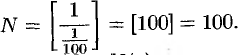
Поэтому иногда записывают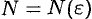 
.
Выясним геометрический смысл определения предела последовательности.
Неравенство (15.2) равносильно неравенствам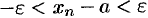 
или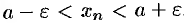 
, которые показывают, что элемент 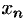находится в 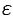-окрестности точки .
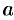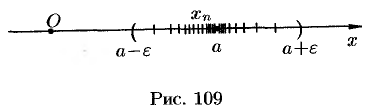
Поэтому определение предела последовательности геометрически можно сформулировать так: число 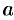называется пределом последовательности 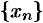, если для любой 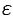-окрестности точки 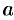найдется натуральное число 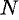, что все значения 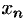, для которых 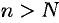, попадут в 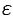-окрестность точки 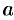(см. рис. 109).
Ясно, что чем меньше 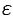, тем больше число 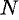, но в любом случае внутри 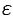-окрестности точки 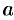находится бесконечное число членов последовательности, а вне ее может быть лишь конечное их число.
Отсюда следует, что сходящаяся последовательность имеет только один предел. Последовательность, не имеющая предела, называется расходящейся. Таковой является, например, последовательность 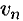(см. с. 128).
Постоянная последовательность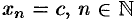 
имеет предел, равный числу 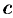, т. е. 
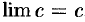. Действительно, для 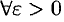при всех натуральных 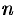выполняется неравенство (15.2). Имеем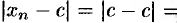 
.
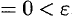На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Уравнения поверхности в пространстве |
| Уравнения плоскости в пространстве |
| Предел функции в точке |
| Односторонние пределы |
