Оглавление:
Определение и основные свойства числовых неравенств.
а) Говорят, что число 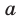 больше числа
больше числа 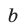 и пишут
и пишут 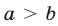 , если разность
, если разность  положительна. Если же разность
положительна. Если же разность  отрица-тельна, то говорят, что
отрица-тельна, то говорят, что 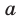 меньше
меньше 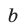 и пишут
и пишут 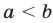 .
.
Запись 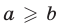 по определению означает, что либо
по определению означает, что либо 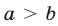 , либо
, либо 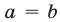 . Аналогично, неравенство
. Аналогично, неравенство 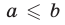 означает, что либо
означает, что либо 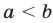 , либо
, либо 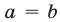 .
.
Неравенства 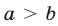 и
и 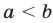 называют строгими в отличие от неравенств
называют строгими в отличие от неравенств 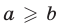 и
и 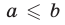 , которые называют нестрогими.
, которые называют нестрогими.
б) Основные свойства неравенств.
1°. Если 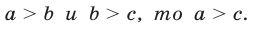
2°. Если 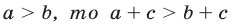 при любом с.
при любом с.
3°. Если 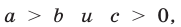 то
то  а если
а если 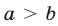 и
и  , то
, то 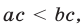 т. е. при умножении обеих частей неравенства на одно и то же положительное число знак неравенства сохраняется, а при умножении обеих частей неравенства на одно и то же отрицательное число знак неравенства меняется на противоположный.
т. е. при умножении обеих частей неравенства на одно и то же положительное число знак неравенства сохраняется, а при умножении обеих частей неравенства на одно и то же отрицательное число знак неравенства меняется на противоположный.
4°. Если 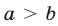 и
и 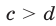 , то
, то 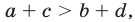 т. е. при сложении неравенств одинакового знака получается неравенство того же знака.
т. е. при сложении неравенств одинакового знака получается неравенство того же знака.
5°. Если 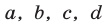 — положительные числа, причем
— положительные числа, причем 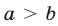 ,
, 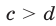 , то
, то  т.е. при умножении неравенств одинакового знака, у которых левые и правые части положительны, получается неравенство того же знака.
т.е. при умножении неравенств одинакового знака, у которых левые и правые части положительны, получается неравенство того же знака.
Эти свойства, сформулированные для неравенств со знаком 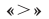 («больше»), остаются в силе и для неравенств, записанных со знаком
(«больше»), остаются в силе и для неравенств, записанных со знаком  («меньше»). Кроме того, указанные свойства справедливы и для нестрогих неравенств.
(«меньше»). Кроме того, указанные свойства справедливы и для нестрогих неравенств.
Наряду с неравенствами вида 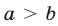 ,
, 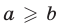 , употребляются так называемые двойные неравенства, т. е. неравенства вида
, употребляются так называемые двойные неравенства, т. е. неравенства вида
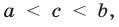
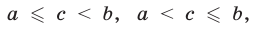
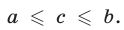 По определению, запись
По определению, запись 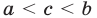 означает, что справедливы (верны) оба неравенства
означает, что справедливы (верны) оба неравенства 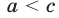 и
и 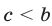 . Аналогичный смысл имеют и другие двойные неравенства.
. Аналогичный смысл имеют и другие двойные неравенства.
К перечисленным свойствам добавим еще некоторые свойства, связанные со степенной функцией.
6°. Если 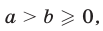 то
то 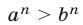 при любом
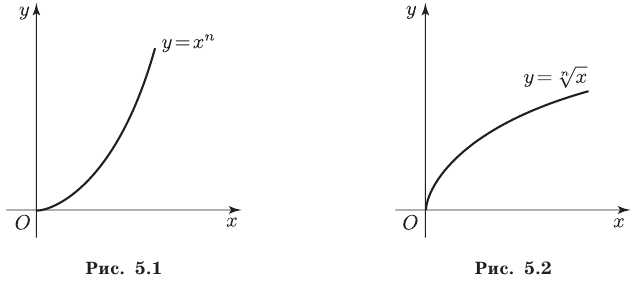
при любом 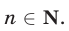 Это свойство выражает тот факт, что функция
Это свойство выражает тот факт, что функция 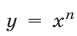 , где
, где 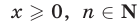 , является возрастающей (рис. 5.1).
, является возрастающей (рис. 5.1).
7°. Если 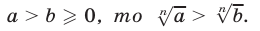
Это свойство иллюстрирует тот факт, что функция 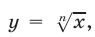 обратная к функции
обратная к функции 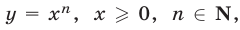 является возрастающей (рис. 5.2).
является возрастающей (рис. 5.2).
Объединяя свойства 6° и 7°, получаем следующее утверждение :
если 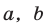 — положительные числа и
— положительные числа и 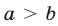 , то
, то 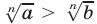 при любом
при любом 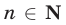 и, обратно, из неравенства
и, обратно, из неравенства 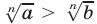 следует, что
следует, что 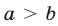 .
.
В этом случае говорят, что неравенства 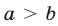 и
и 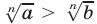 где
где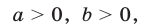 равносильны, и пишут
равносильны, и пишут
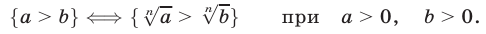
8°. Если 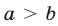 то
то 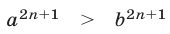 при любом
при любом 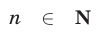 и
и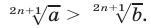
Отсюда следует, что
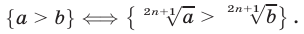
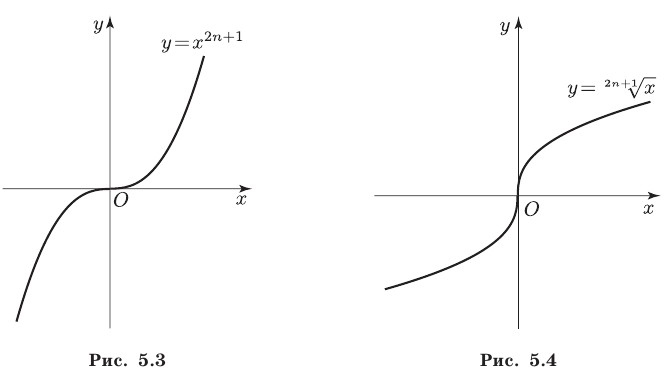
Это свойство выражает тот факт, что функция 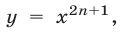
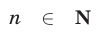 и обратная к ней функция
и обратная к ней функция 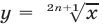 являются возрастающими на всей числовой прямой (рис. 5.3 и 5.4).
являются возрастающими на всей числовой прямой (рис. 5.3 и 5.4).
В частности
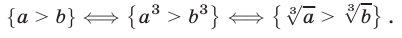
Отметим еще, что неравенство 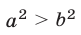 справедливо тогда и только тогда, когда
справедливо тогда и только тогда, когда 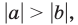 т. е.
т. е.

Отбрасывание знака модуля в правом неравенстве было бы грубой ошибкой.
Некоторые важные неравенства.
1°. Для любых действительных чисел а и b справедливо неравенство
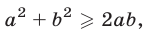
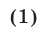
причем знак равенства в (1) имеет место тогда и только тогда, когда 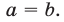
Это утверждение следует из очевидного неравенства 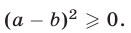 Аналогично доказывается, что неравенство
Аналогично доказывается, что неравенство
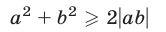
также является верным при любых 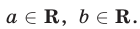
2°. Если а и b — числа одного знака 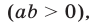 то
то
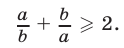
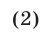
Для доказательства неравенства (2) достаточно умножить обе части неравенства (1) на положительное число 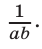
3°. Если 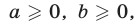 то
то
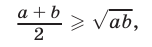
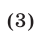
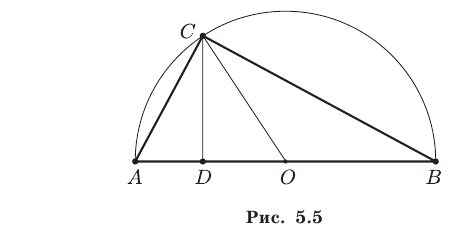
т.е. среднее арифметическое двух неотрицательных чисел не меньше их среднего геометрического. Знак равенства в неравенстве (3) имеет место в том и только в том случае, когда 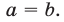 .
.
Неравенство (3) следует из очевидного неравенства 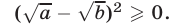
Приведем геометрическое доказательство неравенства (3). Для этого воспользуемся тем, что перпендикуляр CD (рис. 5.5), опущенный из вершины прямого угла С треугольника ABC на гипотенузу АВ, есть среднее геометрическое проекций его катетов на гипотенузу.
Пусть О — центр окружности, построенный на АВ как на диаметре, 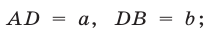 тогда
тогда 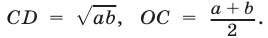 Так как
Так как 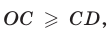 то
то 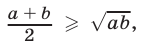 причем равенство в этом соотношении имеет место только при
причем равенство в этом соотношении имеет место только при 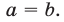 .
.
4°. Неравенство
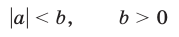
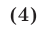
равносильно двойному неравенству
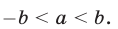
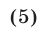
Дадим геометрическое доказательство этого утверждения, пользуясь тем, что 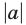 — расстояние от начала отсчета О на числовой прямой до точки А, изображающей число а (рис. 5.6).
— расстояние от начала отсчета О на числовой прямой до точки А, изображающей число а (рис. 5.6).

Неравенство (4) означает, что расстояние от точки А до точки О меньше b, и поэтому число а принадлежит интервалу (—b,b), т.е. справедливо неравенство (5). Обратно, из неравенства (5) следует неравенство (4).
5°. Для любых действительных чисел а и b справедливы неравенства
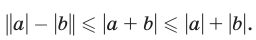
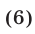
Чтобы доказать правое неравенство (6), запишем очевидные неравенства

Складывая их, получаем неравенство
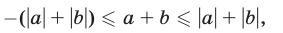
которое в силу утверждения 4° равносильно неравенству
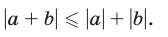
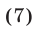
Докажем левое неравенство (6). Используя неравенство (7), получаем
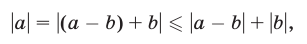
откуда
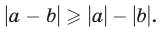
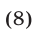
Аналогично
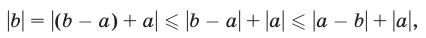
откуда находим
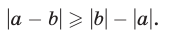
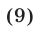
Из неравенств (8) и (9) имеем
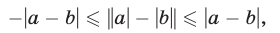
а это неравенство в силу утверждения 4° равносильно следующему:
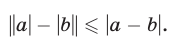
Заменив здесь b на —b и учитывая, что | — b| = |b|, получаем 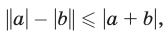
т.е. левое неравенство (6) доказано.
Примеры с решениями
Пример №59.
Доказать, что для любых действительных чисел 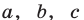 справедливы неравенства:
справедливы неравенства:
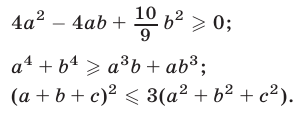
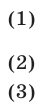
Доказательство. 1) Обозначим левую часть неравенства (1) через А и преобразуем ее, используя метод выделения полного квадрата:
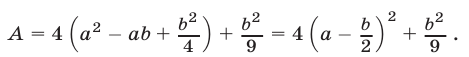
Так как 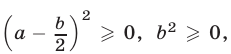 то
то  т.е. справедливо неравенство (1).
т.е. справедливо неравенство (1).
2) Разность В между левой и правой частями неравенства (2) можно преобразовать так:
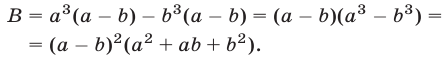
Так как 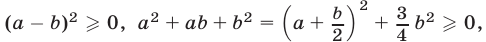 то
то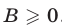 . Неравенство (2) доказано.
. Неравенство (2) доказано.
3) Используя формулу квадрата суммы трех чисел, преобразуем разность С между правой и левой частями неравенства (3):
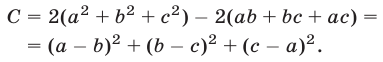
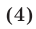
Отсюда следует, что С ^ 0, т. е. справедливо неравенство (3). Заметим, что из равенства (4) следует неравенство
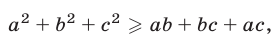
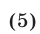
справедливое для любых а, b, с.
Пример №60.
Доказать, что если а,b, с — положительные числа, то
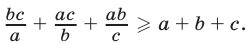
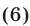
Доказательство. Используя неравенство, связывающее среднее арифметическое и среднее геометрическое двух положительных чисел, имеем
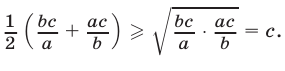
Аналогично
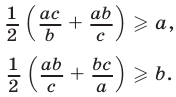
Складывая эти неравенства, получаем неравенство (6).
Пример №61.
Пусть 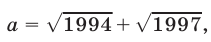
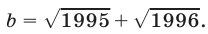 Доказать, что
Доказать, что 
Доказательство. Рассмотрим более общую задачу: сравним числа 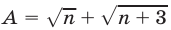 и
и 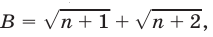 где
где 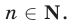 Запишем разность этих чисел в виде
Запишем разность этих чисел в виде
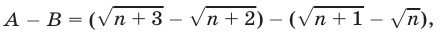
а затем умножим и разделим каждую разность радикалов на их сумму и воспользуемся формулой 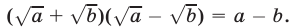 Тогда получим
Тогда получим
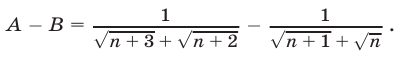
Так как знаменатель первой дроби больше знаменателя второй дроби, то А < B . В частности, а < b.
Пример №62.
Доказать, что при любом 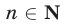 справедливо неравенство
справедливо неравенство
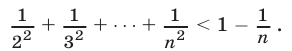
Доказательство. Обозначим через  , левую часть неравенства (7) и воспользуемся неравенствами
, левую часть неравенства (7) и воспользуемся неравенствами
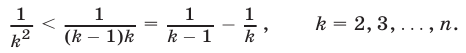
Складывая эти неравенства, получаем
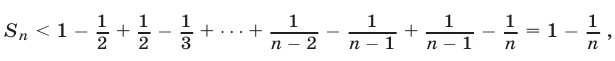
т.е. справедливо неравенство (7).
Пример №63.
Доказать, что при любом 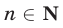 справедливо неравенство
справедливо неравенство
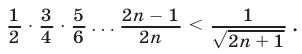
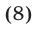
Доказательство. Введем обозначения
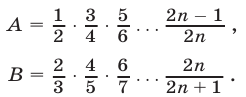
Отсюда следует, что
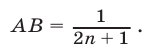
Воспользуемся неравенствами
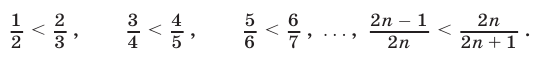
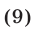
Перемножив неравенства (9), получим А < В, откуда следует, что 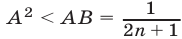 и поэтому
и поэтому 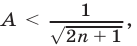 т.е. справедливо неравенство (8).
т.е. справедливо неравенство (8).
Пример №64.
Доказать, что если действительные числа а, b, с удовлетворяют условиям
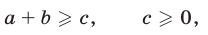
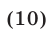
то справедливы неравенства
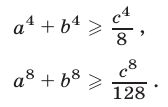
Доказательство. Воспользуемся неравенством
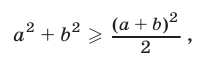
которое равносильно неравенству 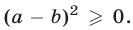 Но из (10) следует, что
Но из (10) следует, что
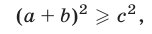
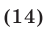
а из (13) и (14) получаем неравенство
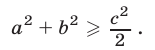

Заменяя в неравенстве (13) а и b на 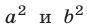 и используя неравенство (15), имеем
и используя неравенство (15), имеем
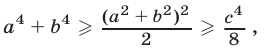
т.е. справедливо неравенство (11).
Аналогично, заменив в неравенстве (13) а и b на 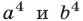 и применив неравенство (11), находим
и применив неравенство (11), находим
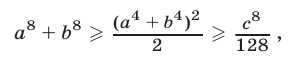
т.е. неравенство (12) доказано.
Пример №65.
Доказать, что если а > 1, то
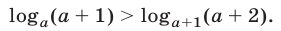
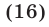
Доказательство. Запишем следующую цепочку равенств и неравенств :
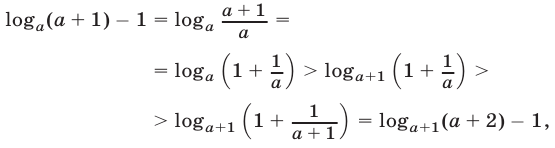
откуда следует, что верно неравенство (16). Здесь мы воспользовались тем, что если а > 1, b > 1, с > а, то 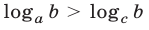 (функция
(функция 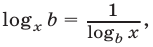 где
где 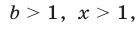 убывает), а также тем, что функция
убывает), а также тем, что функция 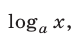 где
где 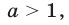 возрастает.
возрастает.
Пример №66.
Доказать, что для любых действительных чисел 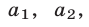
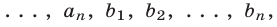 удовлетворяющих условиям
удовлетворяющих условиям

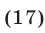
справедливо неравенство
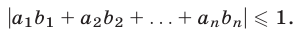
Доказательство. Так как для любых действительных чисел а и b выполняется неравенство 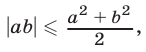 а абсолютная величина суммы не превосходит суммы абсолютных величин слагаемых, то
а абсолютная величина суммы не превосходит суммы абсолютных величин слагаемых, то
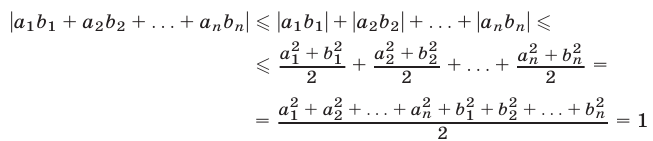
в силу условий (17), т. е. неравенство (18) доказано.
Пример №67.
Доказать, что если положительные числа 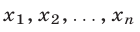 удовлетворяют условию
удовлетворяют условию
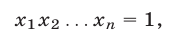
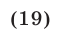
то справедливо неравенство

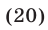
Доказательство. Воспользуемся методом математической индукции. Утверждение верно при 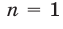 : если
: если 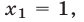 то
то 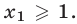 Пусть неравенство верно при всех
Пусть неравенство верно при всех 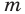 таких, что
таких, что 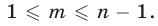 Докажем, что оно верно и при
Докажем, что оно верно и при 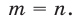
Если все числа 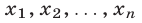 равны единице, то неравенство (20) является верным. Если хотя бы одно из этих чисел больше единицы, то из равенства (19) следует, что хотя бы одно из оставшихся чисел меньше единицы. Пусть для определенности
равны единице, то неравенство (20) является верным. Если хотя бы одно из этих чисел больше единицы, то из равенства (19) следует, что хотя бы одно из оставшихся чисел меньше единицы. Пусть для определенности 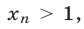
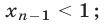 тогда
тогда  откуда следует, что
откуда следует, что
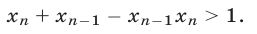
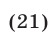
Согласно предположению индукции для любых положительных чисел 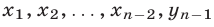 таких, что
таких, что
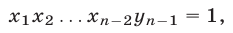
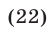
выполняется неравенство
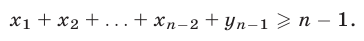
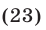
Полагая
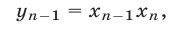
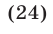
в силу (23) получаем
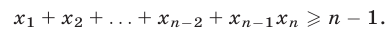
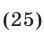
Складывая неравенства (21) и (25), приходим к неравенству (20), справедливому для любых неотрицательных чисел 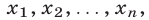 которые (см. (22) и (24)) удовлетворяют условию (19).
которые (см. (22) и (24)) удовлетворяют условию (19).
Замечание. При решении неравенств часто возникает потребность сравнивать числа, записанные с помощью радикалов, логарифмов и т.д. Предполагается, что ответ на вопрос «Какое из двух заданных чисел больше другого?» следует получить без использования микрокалькулятора и других вычислительных средств, а на основании свойств неравенств и свойств элементарных функций.
Пример №68.
Сравнить числа а и b, если:
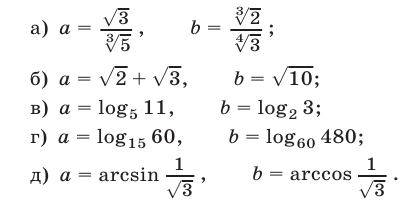
Решение:
а) Обозначим через с разность чисел а и b. Тогда
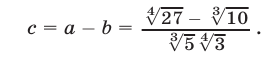
Сравним числа 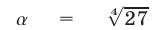 и
и  Так как
Так как 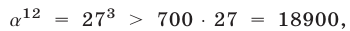
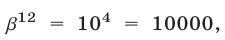 то
то 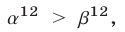 откуда
откуда 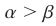 и поэтому
и поэтому 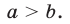
.
б) Так как 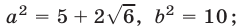
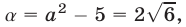
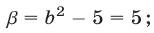
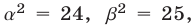 а неравенство
а неравенство 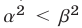 равносильно каждому из неравенств
равносильно каждому из неравенств 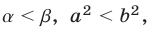 то
то 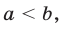 т.е.
т.е.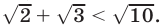
в) Заметив, что 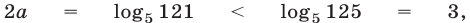
 получим
получим 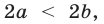 откуда
откуда 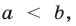 т.е.
т.е. 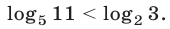
г) Переходя к логарифмам по основанию 2, получаем
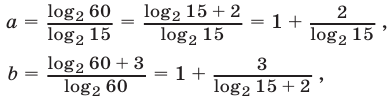
откуда 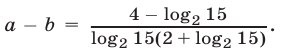 Так как
Так как 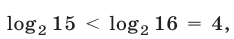 то
то 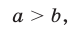 т.е.
т.е. 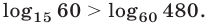
д) Так как 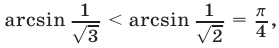 a
a 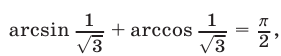 то
то 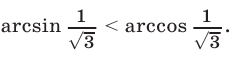
Пример №69.
Упростив выражение
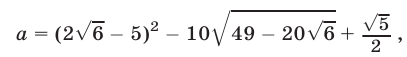
сравнить полученное число с нулем.
Решение:
Так как 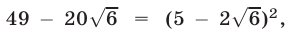 где
где 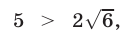 то
то 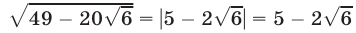 и поэтому
и поэтому
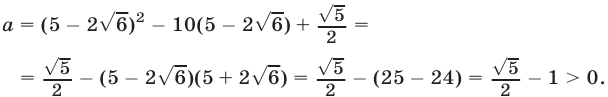
Итак, 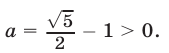
Этот материал взят со страницы решения задач с примерами по всем темам предмета математика:
Возможно вам будут полезны эти страницы:
| Арккосинус с примерами решения |
| Арктангенс с примерами решения |
| Уравнение и его корни. Преобразование уравнений |
| Рациональные уравнения примеры с решением |

