Оглавление:
Числовым рядом называется бесконечная последовательность чисел 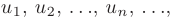 формально соединенных знаком сложения:
формально соединенных знаком сложения:
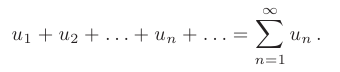
Числа 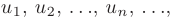 называются членами ряда, а выражение
называются членами ряда, а выражение 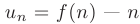 -ым или общим членом ряда.
-ым или общим членом ряда.
Сумма 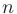 первых членов ряда называется
первых членов ряда называется 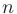 -ой частичной суммой ряда:
-ой частичной суммой ряда:
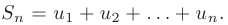
Ряд называется сходящимся, если существует конечный предел последовательности его частичных сумм, являющийся суммой ряда:
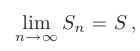
и расходящимся, если указанный предел расходится или не существует
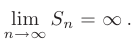
Расходящийся ряд суммы не имеет.
В качестве примеров приведем следующие числовые ряды:
- Гармонический ряд
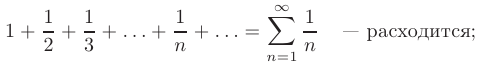
- Обобщенный гармонический ряд
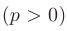
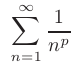
сходится при 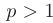 , расходится при
, расходится при 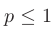 .
.
- Геометрический ряд
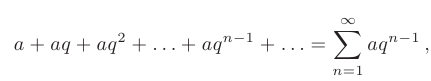
где 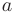 — начальный член;
— начальный член; 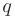 — знаменатель геометрической прогрессии. Геометрический ряд сходится к сумме
— знаменатель геометрической прогрессии. Геометрический ряд сходится к сумме 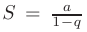 при
при 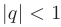 и расходится при
и расходится при  .
.
Знакоположительные числовые ряды
Знакоположительным рядом называется ряд 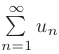 , члены которого неотрицательны:
, члены которого неотрицательны: 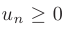 .
.
Необходимый признак сходимости. Если числовой ряд сходится, то предел его общего члена 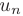 при
при 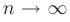 равен нулю:
равен нулю:
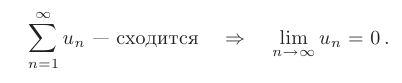
Следствие. Если предел общего члена ряда при 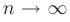 не равен нулю, то ряд расходится:
не равен нулю, то ряд расходится:
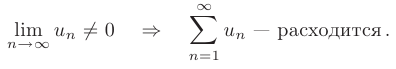
Пример:
Проверить, выполняется ли необходимый признак сходимости для числового ряда
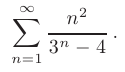
► Для проверки необходимого признака сходимости выпишем и найдем предел общего члена данного числового ряда
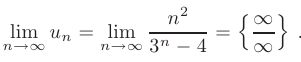
Для раскрытия неопределенности такого типа воспользуемся правилом Лопиталя:
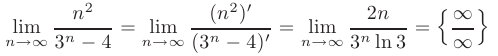
Применяя правило Лопиталя повторно, получим:
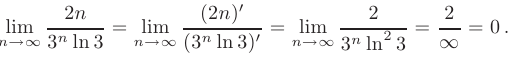
Необходимый признак сходимости для данного числового ряда выполняется, следовательно, расходимость ряда не доказана.
Признак сравнения. Пусть даны два положительных ряда 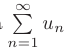 и
и 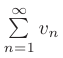 . Если члены ряда
. Если члены ряда 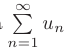 не превосходят соответствующих членов ряда
не превосходят соответствующих членов ряда 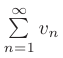 т. е.
т. е. 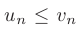 при всех
при всех 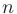 , то из сходимости ряда
, то из сходимости ряда 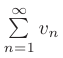 следует сходимость ряда
следует сходимость ряда 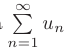 , а из расходимоси ряда
, а из расходимоси ряда 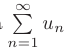 следует расходимость ряда
следует расходимость ряда 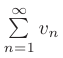 .
.
Пример:
Используя признак сравнения, исследовать на сходимость числовой ряд
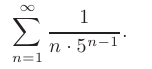
► Сравним данный ряд с рядом 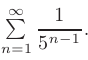 Последний является геометрической прогрессией со знаменателем
Последний является геометрической прогрессией со знаменателем
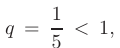
т. е. сходящимся рядом. Так как
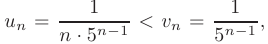
то по признаку сравнения данный числовой ряд сходится.
Предельный признак сравнения. Если для двух знакоположительных рядов 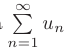 и
и 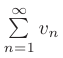 существует конечный, отличный от нуля предел отношения их общих членов
существует конечный, отличный от нуля предел отношения их общих членов
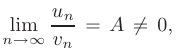
то оба ряда сходятся или расходятся одновременно.
Пример:
Используя предельный признак сравнения, исследовать на сходимость числовой ряд
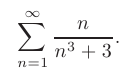
► Если общий член ряда представляет собой отношение двух многочленов, то при подборе эталонного обобщенного гармонического ряда значение 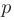 выбирают равным разности наибольших показателей степеней знаменателя и числителя. Так как в нашем случае
выбирают равным разности наибольших показателей степеней знаменателя и числителя. Так как в нашем случае 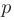 = 3 — 1 = 2. то для сравнения возьмем обобщенный гармонический
= 3 — 1 = 2. то для сравнения возьмем обобщенный гармонический
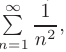
который сходится. Применяя предельный признак, найдем
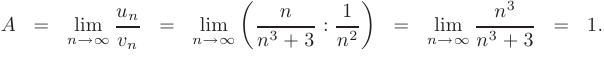
Поскольку предел 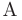 конечен и отличен от нуля, то исследуемый ряд также является сходящимся.
конечен и отличен от нуля, то исследуемый ряд также является сходящимся.
Признак сходимости Даламбера. Если для знакоположительного ряда существует предел отношения 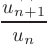 при
при  , то в зависимости от значения этого предела возможны три случая:
, то в зависимости от значения этого предела возможны три случая:
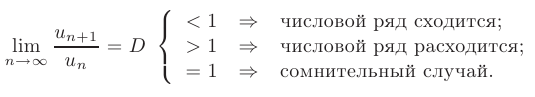
Пример:
Используя признак сходимости Даламбера, исследовать на сходимость числовой ряд
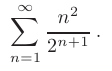
► Для проверки сходимости с помощью признака Даламбера запишем предел отношения (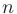 + 1)-го члена к
+ 1)-го члена к 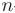 -му:
-му:
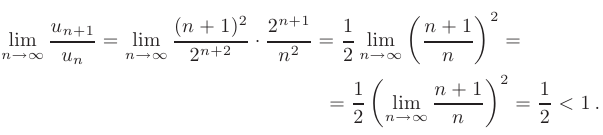
Так как предел полученного выражения меньше единицы, следовательно, данный числовой ряд сходится.
Интегральный признак Коши. Пусть члены знакоположительного числового ряда 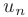 соответствуют при
соответствуют при 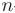 = 1,2,3,… значениям некоторой функции
= 1,2,3,… значениям некоторой функции 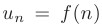 , положительной, непрерывной, монотонно убывающей на интервале
, положительной, непрерывной, монотонно убывающей на интервале 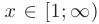 . Тогда несобственный интеграл
. Тогда несобственный интеграл 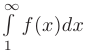 и соответствующий числовой ряд
и соответствующий числовой ряд 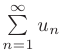 сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
Пример:
Используя интегральный признак сходимости Коши, исследовать на сходимость числовой ряд
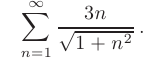
► Для проверки сходимости с помощью интегрального признака Коши запишем формулу общего члена ряда в виде функции натурального аргумента
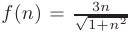
и составим соответствующую ей функцию действительного аргумента
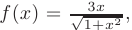
а затем вычислим несобственный интеграл от полученной функции:
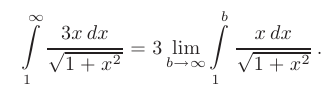
Определенный интеграл, стоящий под знаком предела, вычисляется с помощью подстановки 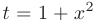 :
:
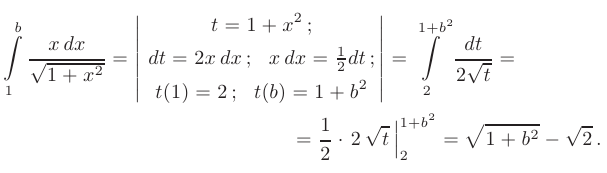
Вычисляя предел полученного выражения, приходим к выводу, что заданный числовой ряд расходится:
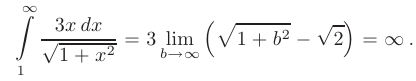
Знакопеременные ряды
Зпакочередующимся числовым рядом называется ряд
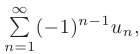
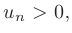
в котором любые два соседних члена имеют разные знаки.
Признак Лейбница. Пусть для знакочередующегося ряда
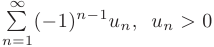
выполнены условия:
- Члены ряда монотонно убывают по абсолютной величине:
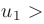
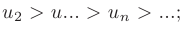
- Общий член ряда стремится к нулю:
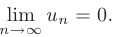
Тогда ряд сходится, причем его сумма 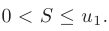
Знакопеременным числовым рядом называется ряд 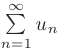 , который содержит как положительные, так и отрицательные члены.
, который содержит как положительные, так и отрицательные члены.
Заметим, что знакочередующийся числовой ряд является частным случаем знакопеременного числового ряда.
Ряд 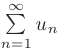 называется абсолютно сходящимся, если сходится числовой ряд
называется абсолютно сходящимся, если сходится числовой ряд 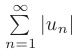 — составленный из абсолютных величин его членов. Сходимость ряда
— составленный из абсолютных величин его членов. Сходимость ряда 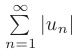 влечет за собой сходимость ряда
влечет за собой сходимость ряда 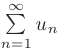 .
.
Ряд 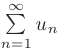 называется условно сходящимся, если ряд
называется условно сходящимся, если ряд 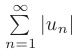 расходится, а исходный ряд
расходится, а исходный ряд 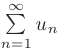 сходится.
сходится.
Пример:
Используя признак Лейбница, исследовать на сходимость знакочередующийся ряд. В случае сходимости ряда, определить тип сходимости.
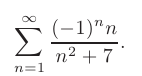
► Для проверки сходимости с помощью признака Лейбница заметим, что при 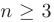 члены данного ряда
члены данного ряда 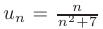 монотонно убывают по абсолютной величине:
монотонно убывают по абсолютной величине:
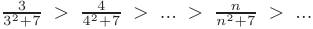
и
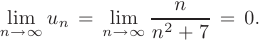
Отбрасывание конечного числа членов не влияет на его сходимость, поэтому по признаку Лейбница ряд сходится.
Определим тип сходимости ряда. Для этого исследуем сходимость ряда, составленного из абсолютных величин его членов:
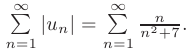
Применяя предельный признак сравнения, возьмем в качестве эталонного ряда гармонический ряд
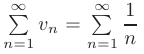
и вычислим предел
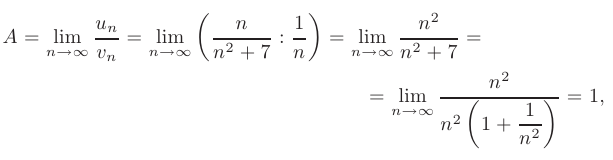
т.е. предел 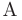 конечен и отличен от нуля. Следовательно, исследуемый ряд ведет себя так же, как и эталонный ряд. Из расходимости эталонного ряда следует расходимость исследуемого ряда.
конечен и отличен от нуля. Следовательно, исследуемый ряд ведет себя так же, как и эталонный ряд. Из расходимости эталонного ряда следует расходимость исследуемого ряда.
Таким образом, сам ряд сходится, а ряд, составленный из абсолютных величин его членов, расходится, т.е. ряд сходится условно.
Этот материал взят со страницы заказа помощи по математике, там можно заказать помощь и ознакомиться с краткой теорией по предмету математика:
Возможно эти страницы вам будут полезны:

