Оглавление:
Числовая последовательность.
а) Если каждому натуральному числу n поставлено в соответствие некоторое действительное число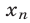 
, то говорят, что задана числовая последовательность (или просто последовательность)
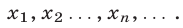
Кратко последовательность обозначают символом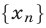 
или 
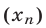, число 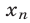, называют членом или элементом этой последовательности, п — номером члена .
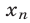б) Числовая последовательность — это функция, заданная на множестве N; совокупность чисел,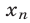 
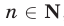, называют множеством значений последовательности.
в) Последовательность обычно задается либо формулой, с помощью которой можно вычислить каждый ее член по соответствующему номеру, либо рекуррентной формулой, позволяющей находить члены последовательности по известным предыдущим.
Арифметическая прогрессия.
а) Арифметическая прогрессия — последовательность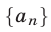 
, определяемая рекуррентной формулой
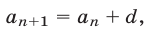
где а и d — заданные числа; число d называется разностью арифметической прогрессии.
б) Для n—го члена арифметической прогрессии справедлива формула
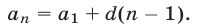
в) Каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому его соседних членов, т. е. при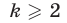 
справедливо равенство
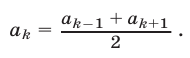
г) Если рассматривается совокупность первых n членов арифметической прогрессии, т.е. числа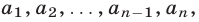 
то сумма каждой пары членов, равноотстоящих от крайних членов этой совокупности, равна сумме крайних членов, т.е. при 
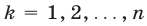справедливо равенство
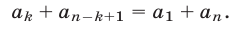
д) Сумма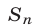 
первых n членов арифметической прогрессии выражается формулой
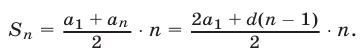
Пример №24.
Найти сумму шести первых членов арифметической прогрессии, если сумма ее первого и пятого членов равна 26, а произведение второго и четвертого членов равно 160.
Решение:
По условиям задачи
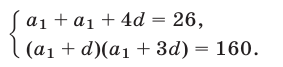
Исключая из этой системы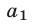 
, где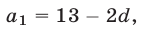 
получаем
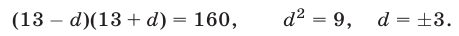
Если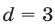 
, то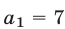 
, а если 
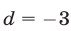, то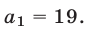 
Искомую сумму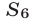 
можно вычислить по формуле
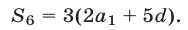
Ответ.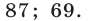 
Пример №25.
Найти отношение суммы первых 2n членов арифметической прогрессии к сумме следующих 2n ее членов, если сумма первых Зn членов равна сумме следующих n членов, а разность d прогрессии не равна нулю.
Решение:
По условию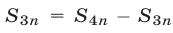 
откуда 
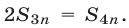Преобразуем это равенство, используя формулу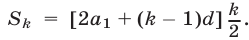 
Получим
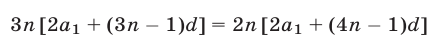
или
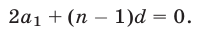
Искомое отношение можно записать так:
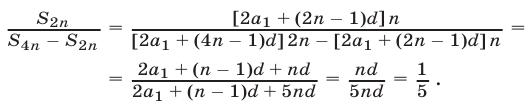
Ответ.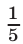 
Пример №26.
Пусть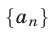 
— арифметическая прогрессия, все члены и разность d которой отличны от нуля. Доказать, что
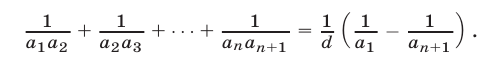
Доказательство. Пусть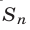 
—левая часть равенства (1). Так как 
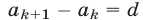при любом k, то
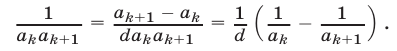
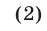
Полагая в (2) k равным 1,2,…, n и складывая получаемые равенства, находим
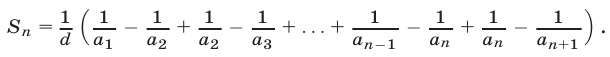(3)
В сумме (3) взаимно уничтожаются все слагаемые, кроме первого и последнего, откуда следует равенство (1).
Этот материал взят со страницы решения задач с примерами по всем темам предмета математика:
Возможно вам будут полезны эти страницы:
| Степень с рациональным и действительным показателем примеры с решением |
| Логарифмы примеры с решением |
| Геометрическая прогрессия с примерами решения |
| Предел последовательности с примером решения |
