Оглавление:

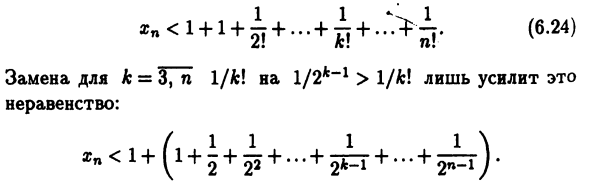




Число е
- Рассмотрим рациональную последовательность {xn} xn = (1 + l / n) n, n∈N. Давайте покажем эту последовательность Увеличение и ограничение. Чтобы рассчитать этот элемент Использовать биномиальное уравнение Ньютона (2.8) N * = 0 Где 0! = 1С * = n! / (Fc! (N-fc)!) Количество комбинаций из n k элементов. xn = И (6.23) ^ = 3, n увеличивается на n-1 единиц (6.23) Количество терминов увеличилось, Предварительно, каждый термин (кроме первых двух), Последовательность {xn} возрастает, zn) 2 Vn ˆ N. (L- (k-1) / n) <1 Vfc> 1, поэтому замените справа Все формулы в скобках для каждой части (6.23), xn <1 + 1 + 1 +. .. + ^ + ..> я. (6,24) & »•
Км Тит Замена. = 3, n 1 / k \ 1/2 * «1> 1 / Ar! Неравенство: xn <1+ ^ 1 + + + + + + В скобках указана сумма первых n элементов геометрии Прогрессия знаменателя q = 1/2 и первого слагаемого a \ = 1 (1.8) Равный 1-V2 «2 тогда 2 1 + 1 + 2J + … + £ y = * b Это соотношение действительно для Vfc € • N. k = n. В результате, учитывая (6.24) и (6.26), xn <zn <e Vn € N: Поэтому теорема о промежуточной последовательности 6.6 Это {gn} = е. Тем не менее, элемент Последовательность {(1 + 1 / n) n} является рациональным числом, а число e Такие, как.
Это трансцендентное и принадлежит Подмножество иррационального множества R \ Q. Это Основана в 1873 году французским математиком С. Эр Мисс (1822-1901). Число е иногда называют не пером. Назван в честь шотландского математика Дж. Нейпира (1550-1617) Составьте логарифмическую таблицу 1 / е. Таблица логарифмов полученной базы е Тогда естественное название опубликовано в Лондоне в 1618 году. Учитель математики J. C Paydel l.
Смотрите также:
| Предел последовательности | Бесконечно малые и бесконечно большие последовательности |
| Признаки существования предела последовательности | Предел функции в точке |

