Оглавление:














Численные методы решения плоских задач газовой динамики. Расчет сверхзвукового обтекания кругового цилиндра
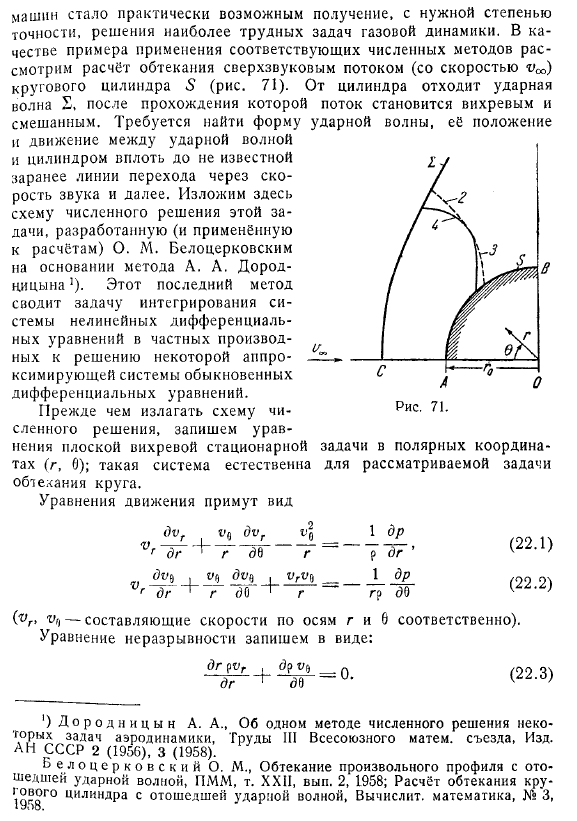
Численный метод решения плоских задач газовой динамики. Расчет сверхзвукового обтекания цилиндра. С появлением электронных высокоскоростных вычислений настоящее время практически возможно получить решение наиболее сложных задач газовой динамики с требуемой точностью. В качестве примера применения соответствующего численного метода рассмотрим расчет обтекания сверхзвуковым потоком цилиндра 5 (рис. 71).
ски возможно получить решение наиболее сложных задач газовой динамики с требуемой точностью. В качестве примера применения соответствующего численного метода рассмотрим расчет обтекания сверхзвуковым потоком цилиндра 5 (рис. 71).
Смотрите также:
От цилиндра отходит ударная волна, после прохождения которой поток становится вихревым и смешанным. Требуется найти форму ударной волны, её положение и движение между ударной волной и цилиндром вплоть до не известной заранее линии перехода через скорость звука и далее. Изложим здесь схему численного решения этой задачи, разработанную (и применённую к расчётам) О. М. Белоцерковским на основании метода А. А. Дородницына.
Этот последний метод сводит задачу интегрирования системы нелинейных дифференциальных уравнений в частных производных к решению некоторой аппроксимирующей системы обыкновенных дифференциальных уравнений. Людмила Фирмаль
Прежде чем излагать схему численного решения, запишем уравнения плоской вихревой стационарной задачи в полярных координатах (г, 0); такая система естественна обтекания круга.
Смотрите также:
Ударная волна выходит из цилиндра и после прохождения, поток превращается в вихрь и является смешанным. Необходимо найти форму ударной волны, ее положение и движение к линии перехода скорости звука, которая не известна до сих пор между ударной волной и цилиндром.
Приведем схему численного решения этой задачи, разработанную Белоцерковским (и примененную к расчетам). Перед описанием схемы численного решения запишите уравнение максимума стационарного поверхностного вихря (v, 0).
Этот последний метод используется для определения решений конкретной приближенной системы нелинейных дифференциальных уравнений оду. Людмила Фирмаль
- Такая система естественна по кругу. Уравнение движения принимает вид (22.1). Адиабатические условия описываются в следующей форме, где как и прежде. Объединяя (22.4) и (22.5), мы приходим к выводу, что 0 зависит только от ф. Уравнение Бернулли, полученное путем объединения (22.1), (22.2) и (22. 4), описывается в следующем виде, как и в плоском случае.
Где ранее (§ 8, стр. 42) критическая скорость, не изменяющаяся при прохождении через поверхность зазора, и поэтому постоянная. Как вихревое, так и не вихревое движение). Умножьте (22.1) на rg и используйте непрерывное уравнение (22. 3), чтобы получить его без проблем.
Если определить плотность из уравнения Бернулли (22.7) через v и g и ввести ее в уравнение неразрывности (22.3), то получим: х = 0. (22. 9 Наконец, используя (22.4), мы получаем отношение для изменения a вдоль определенной линии. Неизвестными функциями здесь являются vr, vh, фb.
Смотрите также:
Давление p и плотность p получены из vr через соотношения (22.6) и (22. 7). Введение адиабатического давления подавления p0 и плотности p0 заторможенного потока (в среде, которая не возмущена) и скрытого скачка температуры записывается. Теперь запишем граничные условия для задачи на разрывной плоскости и обтекаемом цилиндре s.

