Задача 2.1.
Четыре предприятия данного экономического района для производства продукции используют три вида сырья. Потребности в сырье каждого из предприятий соответственно равны 120, 50, 190 и 110 ед. Сырье сосредоточено в трех местах его получения, а запасы соответственно равны 160, 140, 170 ед. На каждое из предприятий сырье может завозиться из любого пункта его получения. Тарифы перевозок являются известными величинами и задаются матрицей
Составить такой план перевозок, при котором общая стоимость перевозок является минимальной.
Решение:
Обозначим через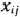 
количество единиц сырья, перевозимого из 
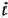-го пункта его получения на 
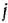-е предприятие. Тогда условия доставки и вывоза необходимого и имеющегося сырья обеспечиваются за счет выполнения следующих равенств:
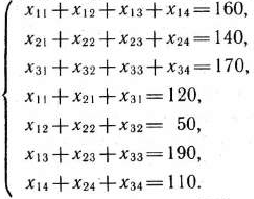
Приданном плане
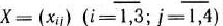
перевозок общая стоимость перевозок составит
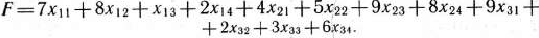
Таким образом, математическая постановка данной транспортной задачи состоит в нахождении такого неотрицательного решения системы линейных уравнений (6), при котором целевая функция (7) принимает минимальное значение.
Эта задача взята со страницы решения задач по предмету «математическое программирование»:
Примеры решения задач по математическому программированию
Возможно эти страницы вам будут полезны:
