Оглавление:
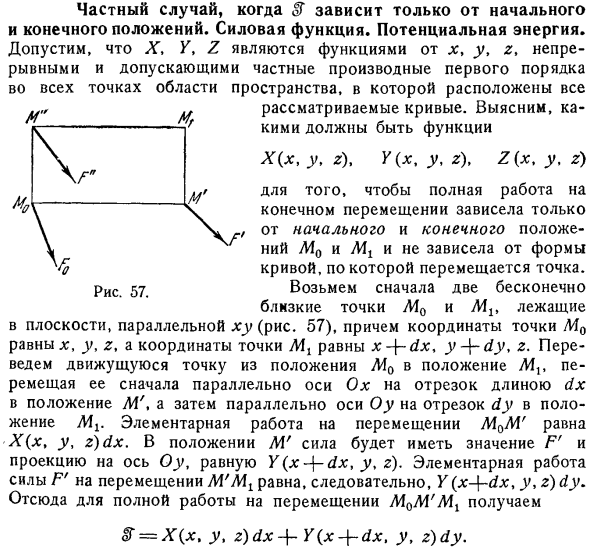




Частный случай, когда ℱ зависит только от начального и конечного положений. Силовая функция. Потенциальная энергия
- Предположим, что X, Y, Z являются функциями x, y и z, которые непрерывно принимают частные производные 1 го порядка во всех точках области. Пространство, в котором расположены все рассматриваемые кривые. Узнайте, какой должна быть функция. Х х, у, Z , к Х, У, Z и Z Х. Y и Z . Таким образом, полная работа конечного движения зависит только от начального положения и конечного положения Io, а не от формы. Кривая, которая движется вдоль точки. Во первых, есть 2 почти бесконечные точки Io и Ir, лежащие вокруг в плоскости, параллельной xy рис.57, координатами точек Mo являются x, y, z, координатами точек являются x dx, y dy, Z.
Ускорения могут возникнуть вследствие того, что точки наэлектризованы или вследствие того, что они друг на друга давят, или вследствие ньютоновского притяжения и т. Людмила Фирмаль
Преобразуйте движущуюся точку из положения L40 в положение Ir, сначала переместите отрезок длины dx параллельно оси Ox и переместите в положение m , затем переместите отрезок DY параллельно оси Oy и переместите в положение Ir y, z .Положение I и величина силы равна F , а проекция на ось Oy равна Y x J dx, y, z. таким образом, основной задачей силы F относительно перемещения является Y x + dx, y, z dy. Для полной работы движения отсюда Afo H hi = X xt y. Z dxY xdx. Г, з ды.
Перемещение точки M в точку, параллельную отрезку dy Oy, сначала перемещает точку, параллельную Oh , в отрезок dx от LG г, з ды + Х Х, Y ды, з ДХ. мы хотим, чтобы оба эти значения eH были equal. To уравняйте их и будьте осторожны с этим Г х ДХ, у, Z = г х, у, Z ДХ Х х. у + dу, Z и= Х Х, Y. з ды После очевидных преобразований ду = дх ДХ делать Делая то же самое в плоскости, параллельной другой координатной плоскости, вы получаете 2 других необходимых условия дз ду ДХ дз до дз ДЗ ДХ Эти условия определены в выражении Xdx г dyz успешно ДЗ Является полной производной функций U от независимых переменных x, y, z.
Если существуют хотя бы некоторые ограничения, то указывают, что эти условия также достаточны. На самом деле, если эти условия соблюдены, то есть идентичность Х DX Дж г ды з ДЗ = ду х, у, Z Оттуда следуют 3 других но ду ду 7 длл L dx do 9 dz Функция U, которая определяется только произвольной аддитивной константой, называется силой function. In в этом случае сила также обладает потенциалом, и ее величина называется потенциальной энергией. Полное действие силы F при прохождении точки Mt вдоль кривой C рис.
- Здесь конечное значение, принимаемое в положении Mi, когда функция U непрерывно изменяется вдоль кривой, а Uo начальное значение функции U в положении MQ. Итак, в области рассматриваемого пространства, если U однозначная функция x, y, z с уникальными значениями в каждой точке этой области, то UQ становится совершенно ясным. И затем Полная работа M from MQ. In в частности, если точка представляет собой замкнутый путь, Mt будет соответствовать A10, и все операции будут равны нулю. Однако если функция U многозначна, например арктангенс, то полная работа не будет полностью независима от пути перехода точки от МО к Ip.
Изменяется в зависимости от величины U. Закрытый Икс= Сколько значение UQ в точке A40 принимается в точке Mlt. Также в этом случае нельзя сказать, что полная работа в замкнутом цикле обязательно будет равна нулю. Однако эти 2 выражения одинаковы.2. два пути C и C от Io до Mt учитываются и показаны o. и cT полная работа в конечном перемещении M0СЛ11 и afoc AFP и полная работа в замкнутом перемещении будет равна ОГ ог. И так оно и есть. =Тогда вся работа равна нулю, а если 0, то она не равна нулю. Например, U = arctg y.
Изучение условий, при которых эти ускорения возникают, является предметом экспериментальной физики. Людмила Фирмаль
Проекция равной силы F В X хп г г = = У2 Представляет собой непрерывную дифференцируемую функцию по всему пространству, расположенному вне цилиндра произвольного малого радиуса, ось которого совпадает с осью Oz рис.59.Функция U представляет собой угол xOP, образованный осью Ox в проекции радиуса радиус вектора OM на плоскость xy. Поэтому, если движущаяся точка представляет собой замкнутую кривую МСМ, которая не окружает ось Oz, функция U, непрерывно изменяющаяся вдоль контура C, принимает начальное значение в точке M, так что общая работа равна нулю.
Однако если точка описывает замкнутую кривую MC M, окружающую ось Oz в положительном направлении 1 раз, то изменение функции U будет равно 2 му, и вся работа также будет равна 2 к. если точка вращается N в положительном направлении вокруг оси Oz, то вся работа будет равна 2 pp. На эти соображения указывает Бертран Journal de 1 eco1e Polytechnique, vol. 28. В общем случае, если у вас есть функция, вы можете установить предложение для выражения, не вдаваясь в слишком длинные детали анализа.
Если функции X, Y и Z не пересекают точки, которые перестают быть дифференцируемыми в ряду, и непрерывная деформация позволяет замкнутой кривой быть нарисованной к точке, то общая работа силы F для этой замкнутой кривой равна нулю. Доказательство этого положения можно легко получить, исходя из следующей формулы: Когда кривая C сжимается до точки P, ее непрерывное положение образует поверхность S. На этой поверхности S, По предположению, функции X, Y, Z конечны, непрерывны и дифференцируемы. Допустимы следующие выражения выражение Ампера Стокса f Xdx + Ydy + ZdZ = f f .dydx + С С Здесь первый Интеграл берется по кривой С, а второй по поверхности S.
Смотрите также:
Решение задач по теоретической механике
| Потенциальная энергия. Механический смысл | Поверхности уровня |
| Полная работа. Единица работы | Замечание о поверхностях уровня |

