Оглавление:

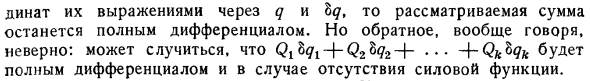

Частный случай, когда выражение возможной работы есть полный дифференциал
- Общий результат, полученный выше, заключается в том, что выражение возможной работы Ци + КЗ 4 + Дь ЧК QP Q2, где… Qk является функцией параметра Q, а параметр QX, q2…. дь. То есть ду дци. В этом случае уравнение дифференциального равновесия совпадает с уравнением, определяющим максимальное и минимальное значения функции U.
Покажем теперь, что оба указанных элементарных действия не изменяют ни главного вектора, ни главного момента относительно произвольной, точки. Людмила Фирмаль
Динамика, если эта функция U действительно имеет максимальное значение для данной системы q, указывает на то, что соответствующее положение равновесия является положением устойчивого равновесия Лежен Дирихле. Если функция силы существует, то есть выражение является 5 х, х,+ г, 8л + 2.82. вся производная функции x J T 2 yy yy … xn Y n rn относится к тому, что просто рассматривается потому что если заменить координаты и производные координат уравнениями через q и Zq, то рассматриваемая сумма останется полной производной.
- Но в общих чертах обратное неверно. Qilqt + К2 К2 + + Если нет полной дифференциальной и степенной функции. Необходимо показать, что шесть деле, присоединение или отбрасывание приложенным в не изменяются. отбрасывание в каждой сумме двух слагаемых, равных по величине и противоположных по знаку. моментов этих векторов — моментом равнодействующего вектора в последних трех суммах. указанных сумм.
Существует бесчисленное множество способов приведения заданной системы векторов к двум векторам. таким двум векторам, из которых один лежит на произвольной прямой, не параллельной главному вектору. Людмила Фирмаль
Система скользящих векторов может быть заменена бесчисленным множеством способов двумя векторами, из которых один проходит через произвольную точку. указанные прямые образуют триэдр. Эти три вектора можно привести к двум. Рп — первоначальные векторы предложенной системы. систем друг к другу.
Смотрите также:
Решение задач по теоретической механике
| Приведение уравнений равновесия к наименьшему числу | Приложения. Тяжелые системы |
| Голономные системы; координаты голономной системы | Принцип Торричелли |

